A SZÁMELMÉLET LÉTFILOZÓFIAI ALAPJAI


A matematika alapelemei a számok, amelyek tulajdonságaival a számelmélet foglalkozik. Ebben az írásomban szeretnék röviden rámutatni a számfajok és az idő, mint fizikai jelenség kapcsolatára, hogy bemutassam, milyen (kevéssé ismert) létfilozófiai alapjai vannak a matematikának és hogyan kapcsolódik a számok tudománya a gyakorlati fizikához. A leírások természetesen nem tükrözik a tudomány mai és holnapi álláspontjait, a megértésükhöz pedig szükséges ismerni az időfizika és létfilozófia rendszerét.

1. A SZÁMFAJOK

A természetes számok valódi összességek absztrakciói, amik függetlenek az összességek elemeinek különféle tulajdonságaitól, valamint a jelölésükhöz használt szimbólumoktól. Az 1, 2, 3... természetes számokat tőszámneveknek nevezzük, ami számlálási eredetükre utal (pl.: három ember). Ha a természetes számokat valamely halmaz elemeinek megszámozására használjuk, akkor sorszámnevekről beszélünk (pl.: harmadik ember). A természetes számok közé tartoznak a pozitív egész számok és a nulla. Egyes matematikusok a nullát nem sorolják a természetes számok közé, mivel a nulla a semmi reprezentánsa, a semmi pedig (mint a valami hiánya) nem létezik (a természetben).
Két természetes szám összege és szorzata mindig természetes szám. Különbségre és hányadosra ez a megállapítás csak speciális esetekben érvényes, ezért a természetes számok körét úgy kell kibővítenünk (újabb számok hozzáadásával), hogy a kivonás mindig elvégezhető legyen. Ehhez szükséges a plusz és mínusz előjel bevezetése, ami a számokat a pozitív és negatív számok csoportjába sorolja. A pozitív és negatív egész számok a nullával (ami a semmi helye a számegyenesen) együtt alkotják az egész számokat. Ha nem tüntetjük fel egy szám előtt az előjelét, akkor alapértelmezésben pozitív számról van szó.
Ahhoz, hogy az egész számok osztása korlátlanul megoldható legyen, a halmazukat ki kell egészíteni a racionális számok halmazával, közismertebb nevükön a törtekkel. Minden racionális számnak megfelel a számegyenes egy pontja és két racionális szám között mindig tetszőlegesen sok további racionális szám van. A racionális számok körében a négy alapművelet (összeadás, kivonás, szorzás, osztás) korlátlanul elvégezhető.
A magasabb fokú műveletek korlátlan elvégzéséhez (pl.: hatványozás, gyökvonás) a racionális számokat ki kell egészíteni az irracionális számok halmazával, amilyenek például a gyök 2, lg 2, Pi, e. A racionális és irracionális számok együtt alkotják a valós számok halmazát, amelyek körében minden pozitív valós szám gyöke kiszámítható.
A negatív számból vont páros kitevőjű gyök értéke azonban nem valós szám (pl.: gyök -1), mert nincs rajta a számegyenesen, így a valós számok körét ki kell egészíteni a képzetes számokkal, amelyek összessége alkotja a komplex számok halmazát. A komplex szám egy valós és egy képzetes részből áll, ami a képzetes egység együtthatója. A komplex számok körében minden számolási művelet korlátozás nélkül elvégezhető és ezek geometriailag a Gauss-féle számsík pontjaiként ábrázolhatók (a számegyenes két oldalán).
A komplex számok négy dimenzióra történő nem kommutatív (nem felcserélhető) kiterjesztésével kapjuk a kvaterniókat, amik négy báziskvaternió lineáris kombinációjaként írhatók fel. Ezek arra használatosak, hogy a tisztán képzetes számokkal leírható a három dimenziós vektortér, vagyis a három dimenziós (időbeli) mozgások.
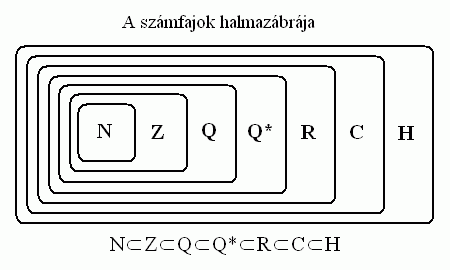
Ahhoz, hogy a számfajok egymással való kapcsolatát könnyebben megérthessük, íme a viszonyuk halmazos ábrázolása (1. ábra). Az egyes betűk jelentése: természetes számok: N, egész számok: Z, racionális számok: Q, irracionális számok: Q*, valós számok: R, komplex számok: C, kvaterniók: H.


2. A SZÁMFAJOK LÉTFILOZÓFIAI ÉRTELMEZÉSE

A 0D-s jelenpont (Mandu) önmagában csak van, de nem létezik, ezért megfelel a nullának. Két jelenpont ha kölcsönhatásba lép egymással, akkor létezni kezdenek egymás számára és együtt egy létező pontot (Bindu) alkotnak, ami megfelel az egynek, mint legkisebb természetes számnak. Az egy, mint szám egyben az egységnyi távolságot is meghatározza a számegyenesen a nulla és az egy között. Ez a távolság fizikailag egy mértékegység nélküli alapmérték, éppen ezért nincs értelme a nagyságát firtatni. Ha a létezőhöz csatlakozik egy harmadik jelenpont is, akkor a három pont tétel értelmében megjelenik a különbség fogalma, ami a számegyenesen a kettőnek felel meg. Mivel a kettő messzebb van a nullától, mint az egy.
Az a tény, hogy két jelenpont egymás számára létezve egy két irányba nyúló primer időszálat generál (vízvonalat) azt jelenti, hogy az idő folytonos, és a forgásnak köszönhetően egyben kvantálható is, miként a számegyenes. A forgásnak ekkor még nem értelmezhető az iránya, tengelye és sebessége, tehát csak annyi állapítható meg, hogy a Binduban az egyik Mandu forog (helyzetváltoztatást végez) a másikhoz képest. Ha a szál nyúlását kifelé értelmezzük a kezdő állapottól, akkor kapjuk az egész számok egyenesét (negatív és pozitív számok, valamint a nullapont). Ha viszont befelé értelmezzük a két létező között, akkor kapjuk a tört számok egyenesét a nulla és az egy között. Mivel külső viszonyítási rendszer hiányában nem dönthető el, hogy az időszál kifelé nyúlik vagy befelé strukturálódik, mindkét folyamatot logikusan (racionálisan) egyenértékűnek kell elfogadnunk. Így kapjuk meg a primer időszálból a racionális számok halmazát.
A jelenpontokból kiáradó sajátidő a múlttér, beáradó jövőtér ugyanakkor nem létezik. Ezért a számegyenes fizikailag csak félegyenes lesz, ami az egytől (létező jelen) indul és egy irányba tart, mivel az időnek csak egyféle telési iránya van. A természetes számok körébe ezért nem tartozik bele a nulla, sem a negatív számok. A misztikusok szerint egyébként az Isten csak (pozitív) egész számokat használ a teremtése során, és a teremtés minden pillanatában véges méretű, bár folyamatosan növekszik, terjed kifelé a végtelenbe.
Ahhoz, hogy a negatív számok létrejöhessenek (megteremtődhessenek), szükség van arra a tényre, hogy az időhullámok terjedési sebessége (emanáció) egységnyi legyen, azaz véges mértékű. Ekkor a jelenpontok egymásra gyakorolt sugárirányú sodrása tachion sebességre löki a jelenpontokat, amik kúpos szerkezetű hullámterében a kettős idősűrűség virtuálisan létrehozza a két irányba nyúlni látszó időszálat. Ez az időszál (tűzvonal) a tachion múltterébe belépő szemlélőpont számára létezik és a nulla pontja a szál töréspontján található. A tűzvonal abban különbözik a vízvonaltól, hogy a vízvonal a keltő forrásai számára látszódik, a tűzvonal pedig más jelenpontok számára is látszódhat, nem csak a keltője (tachion jelene) számára.
A racionális számoktól két módon juthatunk tovább a számfajok bővítése terén. Egyrészt azáltal, hogy a tűzvonalat keltő jelenpont (a Teremtő Atya) önmagába visszakanyarodva meglátja a tűzvonalat, és szerencsés körülmények között létrehozva az első időhurkot, végtelen ciklusba zárja a saját szemlélő tudatának virtuális másolatát. Ezen eleven szemlélő, az Isten számára a tűzvonal egy belőle két irányba kifutó élvonal lesz, aminek pozitív része a jelenpont felé nyúlik, negatív része pedig a régmúlt feneketlen mélységébe. Az Isten, mint főszerán azonban irracionális módon mégsem tekinthető a számegyenes nulla pontjának, mivel több virtuális tachionból áll és a mozgását folyamatosan háborgatja az őskáosz hullámtere, szétmosva létezésének jelenét egy jelenszakasz mentén.
Mivel az időhullámok sodrása a sűrűségük függvénye, ami a jelenpontjuk kibocsátáskori mozgásállapotától függ (idődoppler), és mivel ez a sűrűség tetszőleges értéket fölvehet a fizikailag lehetséges tartományon belül, az elért jelenpontokra gyakorolt hatásuk is tetszőleges lehet. Ez a sűrűség moduláció az elért jelenpontok számára információt hordoz (a forrásáról), amely a létezők transzcendens mivolta révén soha nem szaturálódik (telítődik). Így tehát egy távolságtartományon (téridőben értelmezett időszál szakaszon) belül egy jelenpont helyzete bármely racionális és irracionális értéket fölvehet.
A másik lehetőség a számfajok bővítésére az, ha a Teremtő Atya tachionjának hullámterébe egy másik jelenpont szalad bele és jelenik meg a számára a tűzvonal káprázata. Ez fizikailag egyenértékű azzal, ha az első lehetőséget tovább gondolva, az Isten teremtményeket, azaz további időhurkokat másol önmagából, akik számára az egész belátott létrendszer fa-gráf szerűen elágazó időszálai alkotják a káprázatot. Az irracionális számok tehát fizikailag a jelenpontok közti irracionálisan változó hullámtérbeli távolságoknak felelnek meg, amit a halmazperturbáció okoz. A racionális számok pedig fizikailag az időhurkok jelenpontjait összekötő időszálaknak felelnek meg.
Másfelől szemlélve a létrendszert azt látjuk, hogy a természetes számoknak fizikailag egy tetszőleges jelenpont számára egyszerre létező (látott) többi jelenpont darabszáma felel meg. Mivel ez csakis megszámlálhatóan végtelen sok lehet (pozitív egész szám), bármely konkrét időpillanatban. A megszűnő jelenpontok után visszamaradó létszünetek, mint növekvő semmi buborékok (amik körül az árvahullámok tágulnak) pedig megfelelnek a nullának.
A racionális és irracionális számok együtt alkotják a valós számok halmazát, ahogyan a teremtésben az okforrások és virtuális források, hullámtéri távolságok és időszál folytonosságok együtt alkotják a valós (megfigyelhető) létezés halmazát. A komplex számok halmaza a valós számok képzetes számokkal történő kiegészítésével jön létre, kiterjesztve a számegyenest egy számsíkká. Fizikailag ez megfelel a teremtés jövőterében leendő dolgok (lehetőségek) összességének, amik még egyetlen szemlélő jelenpont számára sem léteznek, de sejthető (számítások révén előre jelezhető) a megjelenésük. Nyelvtanilag a képzetes számok megfelelnek a befejezett jövő időnek. A „képzetes” szó azt jelenti: „látszólag képzett”, vagyis „valamiről virtuális képet létrehozott”. Ennek köszönhető, hogy a bizonytalan jövő is elképzelhető (fantáziálás), bár a megvalósulása (a számegyenesre történő leképzése!) természetesen egészen más lesz, mint az elképzelése.
A képzetes számok számsíkjának további kiterjesztésével jön létre a kvaterniók négy dimenziósnak nevezett számtérideje, amiben az egy valós számhoz (ami az időszálra esik) hozzárendelünk három képzetes számot (amik a szál körüli 3D-s tér meghatározott pontjainak felelnek meg). Fizikailag ez megfelel a téridő hullámterében definiált térdimenziónak, ami valójában csak időből áll, tehát mint tér, pusztán képzetes jelenség.
A kvaterniókkal végzett műveleteknél fellép a műveleti sorrend felcserélhetetlensége, ami megfelel annak a tapasztalatnak, hogy a téridő hullámterében a szemlélők által észlelt időbeliség szigorúan lineáris, vagyis hétköznapi megfogalmazásban: az idő telése egy irányú és nem megfordítható. Ez a tulajdonság nem érvényes az őskáoszra (nemtér-nemidőre), ahol az időszálak (valós számok egyenese) húzódnak, mivel ott az ősidő hullámtere nem ciklikusan ismétlődő és kényszerítő (rendező) erejű.
A műveleti sorrend felcserélhetetlensége továbbá megfeleltethető az aszimmetria tétel fizikai következményeinek is. Annak a ténynek, hogy a teremtésben minden hely és idő egyedi és megismételhetetlen, s ezáltal a dolgok nem keverhetők össze egymással. Tehát egy adott eredmény elérése csakis és kizárólag egyféle útvonalon lehetséges a létezésben.
Összefoglalva: Amint az látható, a matematikai számelmélet teljes pontossággal leképezi az időfizika törvényeit és a teremtés természetes rendjét, összhangban a létezés szerkezetével. A számelméletet megalapozó filozófiát pont azért nem tudták a mai napig se rendesen megalkotni a matematikusok, mert nem rendelkeztek kellő mélységű ismeretekkel a teremtésfilozófiáról. Ezt a fontos hiányt most pótoltam, mindenki okulására.

Készült: 2009.08.21.

Következő írás

Vissza a tartalomhoz