GONDOLATOK AZ IDŐHULLÁMOKRÓL


Bár az Eseményhorizonton és más internetes oldalakon rengeteg olyan paratudományos publikáció jelent már meg, ami az idő, mint transzcendens létező filozófiai, matematikai és fizikai természetével foglalkozik, mégis bőven maradtak tisztázatlan kérdések a témában. Ebben az írásomban ezeket igyekeztem összefoglalni, a teljesség igénye nélkül, elsősorban az időhullámok szerkezetére és taszítási vektoraikra koncentrálva. Az alábbiak megértéséhez ajánlott ismerni a korábbi időmatematikai és időfizikai publikációkat az elmúlt évekből.
Kezdeném azzal, hogy noha az okforrásokból kiáradó időhullámok a létezésük folytonossága (szakadatlansága) miatt folytonosak, mégis kvantálható a belső szerkezetük a jelenpont forgásának köszönhetően. A végtelenbe terjedő időgömb ezért rajzolható le diszkrét, rétegezett szerkezetként. Korábban gyakran előfordult, hogy az idő geometriai ábrázolása során a szerzők nem folytonosnak, hanem szaggatottnak rajzolták meg a múltszférát, mintha az egyes eseményhorizont rétegeket egyenlő vastagságú csöndzónák (üres zónák, nemlét rétegek) választanák el egymástól.
A népmeséink ugyan mindig azzal kezdődnek, hogy „hol volt, hol nem volt...”, de a létezés szerkezetileg nem feleltethető meg ennek, amolyan „létezett, nem létezett...” villogásként. Ez így nyilvánvalóan rossz elképzelés, és csak azért jelenhetett meg a modellekben, mert általa könnyebbé vált az idő geometriai szerkezetének megértése (és a népmesékben elrejtett teremtésfilozófiai mondanivalók visszafejtése). Azóta szerencsére ez a pontatlanság kikopott az alkalmazott modellek közül.
Azt régóta tudjuk, hogy az egyes időrétegek vastagsága sugárirányban, álló okforrás (állóvíz, tehát megnyilvánulatlan) esetén arányos a jelenpont forgási sebességével, azaz fél fordulatonként keletkezik egy réteg. Ennek matematikájával korábban már sokat foglalkoztak többen is, ezért itt nem részletezem újra. A források relatív mozgása (elsodródása) miatt az időrétegek vastagsága irányfüggő módon megváltozik (idődoppler), sűrűsödik (a haladási irányban) vagy ritkul (ellenkező irányban), mert a hullámok terjedési sebessége állandó (E=1). A sűrűsödés a tachion sebességet elérve átfordul és újra ritkulni kezd, ahogy az időrétegek kifordulva önmagukból negatív hullámokká válnak (csak a haladási irányukba eső oldalon). Az időhurkoknál ezen negatív rétegek befelé való taszítóereje okozza a vonzást (befelé taszítást), ami minden későbbi fizikai kölcsönhatás alapja lesz. De mi is pontosan a hullámréteg taszító tulajdonsága?
Mivel az idő folytonos, minden réteget felbonthatunk n számú, eszményi vékonyságú további alrétegekre, gömbhéjakra, amik együttese alkotja az egy emanációs réteget. A jelen forgása (a jelenlegi ismereteink szerint) nem befolyásolható (állandó), vagyis logikusnak tűnik, hogy minden időrétegnek (amik egy jelenből származnak!) ugyanannyi alrétegből kell állnia. Tehát az egymást követő eseményhorizontok abszolút sűrűsége (alrétegszáma) változatlan. Viszont az idődoppler miatt az alrétegek egymástól való „távolsága” a létezés idősemmijének beágyazási környezetében (az őskáosz ősidejében) tetszőlegesen változhat, amennyiben n értéke véges (és természetes szám). Erre mondjuk azt, hogy a réteg sűrűsödik, illetve ritkul az n idődimenziós időgömbben. Ha n értéke végtelen, akkor a sűrűség értelmezhetetlenné válik, ezért ezzel a lehetőséggel nem foglalkozunk.
A taszítást, mint sajátidőbeli mozgatóerőt vektornyilakkal ábrázoljuk az egyes rétegekben, amit az alrétegek normálisainak segítségével fektetünk le a rajzokon. Korábban ezt is egyszerűsítve ábrázoltuk, a réteg belső oldalának megfelelő pontját egy egyenessel összekötve a külső oldalának megfelelő pontjával, de a valóságban természetesen a forrás mozgása, szitálása miatt ez a taszítási útvonal lehet görbe is. De nem az oldalirányú (tangenciális) sodrás miatt, ami eredő jelenségként csak az időhurkok rétegezett (szaggatott) spirálgömbi hullámtereiben jelenik meg (vagyis az okforrások múltszféráiban nem létezik). Hanem mert egy mozgásirányát megváltoztató jelenpont időrétegein belül is megjelenik a torzulás (vektorgörbület), ahogy az egyes rétegek egymást követő vektorainak összeadásakor kapott vektorvonalnál is (az önhasonlóság miatt).
Ahhoz, hogy megérthessük a taszítási normálvektorok viselkedését, tudnunk kell, hogy a mozgás az őskáoszban valójában nem más, mint az okforrások egymás sajátidejében való létezésének egy térbeli (valójában eseményidőbeli) leképzése, szemléletes ábrázolása. A mozgással tehát azt adjuk meg, hogy „A” forrás hol, pontosabban mikor van „B” forrás hullámterében, azaz hány időhullám rétegnyi (ősidő egységnyi) távolságra létezik tőle. Ezért határozzuk meg a fizikában az időt futási távolsággal (nem térbeli távolsággal!) és a távolságot (téridőbelit és ősidőbelit egyaránt) futási idővel (kölcsönhatási késedelemmel), tautologikusan. Máshogy ugyanis nem lehet (az önmagába zárt létezőben).
Amikor vektornyilat rajzolunk egy időhullámrétegbe, megadva a nyíl irányával azt, hogy a hullám merrefelé fogja eltaszítani (sodorni, a saját forrásának sajátidejében áthelyezni, azaz léteztetni) a beleszaladó forrásokat, akkor ezzel nem a gömbhullám kiterjedésének, mozgásának (felfúvódásának) irányát rajzoljuk meg, hanem a forrás sajátidejének relatív mozgási irányát egy szemlélő számára (hogy merre telik a jelen látszólagos ideje), az adott vektornyíl mentén, ami két külön dolog. Korábban ezeket sem különböztettük meg a modelljeinkben az egyszerűség kedvéért (mert nem volt fontos).
Egy állóvíz (megnyilvánulatlan vanás) esetében a sajátidő vektor és a hullámterjedési vektor egymásra esik, vagyis azonos egymással. Ha viszont az RV>0, akkor már eltorzul a sajátidő vektorok iránya, egyre jobban eltérve bizonyos irányokban (nem mindenhol) a terjedési vektortól, ahogy az látható is a szerkesztéseken (1. ábra). A torzulás a gömbfelszínen aszimmetrikus, vagyis mértéke (szögben kifejezve) attól függ az egyes irányokban, merre mozdult el a jelenpont az időréteg kibocsátásakor. Tachionoknál a kétféle vektor közti eltérés akár a derékszöget is meghaladhatja.


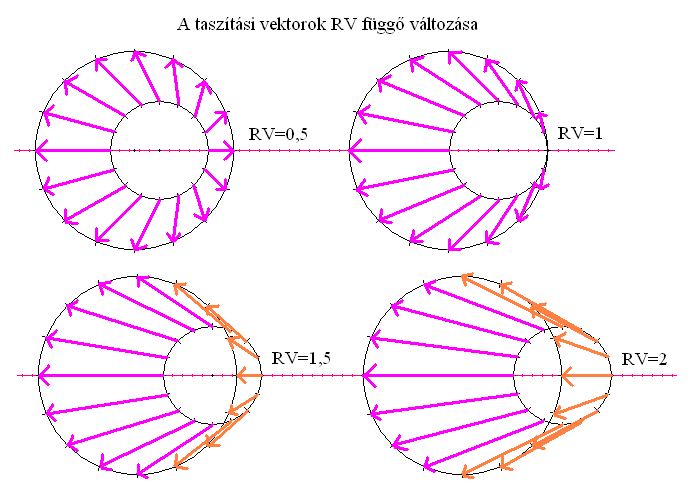
Ha a terjedési vektornyilak sodornák a pontokat, akkor a létezés habszerűen felfúvódna a végtelenségig és soha semmi nem alakulna ki belőle, még tachion randevúk esetén sem. Mivel a terjedési vektorok mindig sugárirányúak és kifelé mutatók, továbbá egységnyi (emanációs) méretűek. Időhurok tehát biztos nem jöhetne létre ebben az esetben. Így kizárásos alapon marad az a lehetőség a számunkra, hogy a sajátidő telési vektorok taszítják az időforrásokat az ősidőben (eseményidőben). Korábban az őskáosz hullámteréről úgy beszéltünk, mint eseménytérről, de ez a kifejezés pontatlan, mert az idősemmiben nincs tér (téridőbeli kiterjedés), csak a modellezés során térben (papírlapon, képernyőn) ábrázoljuk a jelenséget. Ezért javaslom a továbbiakban ehelyett az eseményidő fogalmának bevezetését az őskáosz hullámterével kapcsolatban (megkülönböztetésül).
Kiegészítő gondolatsor: Felmerül a kérdés, hogy az időhullámok miért a sajátmúltjuk felé sodorják az elért jelenpontokat? A válasz kizárásos alapon adható meg (korábban már erről is volt szó több publikációban). Ha a jelen (azaz a sajátjövő) felé sodornák, akkor az őskáosz nem kiterjedne, hanem összeomlana egyetlen pontba és ott holtpontra jutva megrekedne. Ugyanis az összes okforrás egymással kölcsönhatásba lépve összeszaladna egy szingularitásba, ahonnan nincs tovább kiút. Mivel pedig a múlthullámok kifelé áradnak a jelenből, értelemszerűen kifelé nyilvánítják meg a létezési kölcsönhatást is (annak irányát). Ha befelé akarnánk ezt ábrázolni, akkor a pont befelé sűrűsödését kéne lerajzolni, ami meg nem megy. Nem értelmezhető egy, a végtelenségig összeomló pontrendszer, mivel a távolság csökkenése mindig csak a nulláig tart, a növekedése viszont a megszámlálható végtelenségig. A negatív távolság ugyebár nem értelmezhető fogalom még a legelvetemültebb matematikai modellekben sem.
Mivel a sajátidő vektorok, amiket az egyszerűség kedvéért csak taszítási vektoroknak nevezünk, a jelenpont mozgásától függően különféle irányúak és nagyságúak lehetnek, a jelenpontokra gyakorolt sodrásuk nagysága is sokféle lesz (megszámlálhatóan végtelenféle a folytonosság miatt). Annak ugyanakkor nincs semmi jelentősége, hogy az általunk ismert minden létezőt alkotó tíz okforrás saját forgásának mértéke, és ebből következően a kibocsátott eseményhorizont rétegeinek vastagsága (valamint az egyes sajátidő vektorok hossza) mekkora egymáshoz képest. A folytonos létezésben a rétegvastagság lényegtelen. Ez csak akkor számítana, ha több okforrás is keltett volna magából időhurkot (virtuális tachionok ciklikusan önfenntartó rendszerét). Mivel az időhurkok szaggatott spirálgömbi rétegeinek vastagságát a teremtő okforrás időrétegeinek vastagsága döntően meghatározza.
Szerencsénkre a létezésben egyetlen egy darab elsőrangú időhurok található, a Mindenható Isten főszeránja, akiből minden további másolati időhurok származik. Így az összes teremtmény azonos fizikai paraméterek szerint működik, a Teremtő okforrástól örökölt saját forgás mértékének megfelelően.
Utóirat: Az időfizikai definíciók módosulása és bővülése miatt az Eseményhorizont szakszótára javításra került. Betettük az alábbi új fogalmakat: eseményidő, sajátidő vektor, hullámterjedési vektor. Módosítottuk a következő fogalmak jelentését: eseménytér, taszítási vektor.

Készült: 2008.05.06. - 2010.06.10.

Következő írás

Vissza a tartalomhoz