KÖRBEJÁRÁSI ÚTVONALAK


1. ELŐSZÓ

Az Életfa elágazó időszál rendszere könnyen ábrázolható fa-gráffal. Az egyes csomópontjait alkotó időhurkok pedig a ciklikusságuk miatt jól modellezhetők körgráfokkal, annak ellenére, hogy fizikailag nem zárt körök, hanem nyitott körívek. A körgráfok matematikai tulajdonságaival 2004-ben kezdtem foglalkozni, fontos felismerésekre jutva velük kapcsolatban, majd a kutatási eredmények (egyéb elfoglaltságaim miatt) raktárba kerültek és betemette őket az irathalom. Csak most jutottam el odáig, hogy ismét elővegyem az anyagot, miután olvastam A triquetra titka (2010) című írást az Eseményhorizonton. Az ok a valknut (Ódin-csomó) ezoterikus jelentésének felismerése vala, ami néhány hét alatt elvezetett ennek a publikációnak a megírásáig.
Az alábbiakban röviden ismertetem a körgráfok körbejárási útvonalaival kapcsolatos matematikai, időfizikai és nyelvészeti tudnivalókat, aminek megértéséhez nem árt ismerni a korábbi cikkeket az Eseményhorizonton. Elsősorban Az energiakvantumok geometriája (2007), Az Életfa szerkezete (2008) és Az időhurok kétféle modellje (2009) címűeket.

2. A KÖRGRÁF KÉSZÍTÉS SZABÁLYAI

A körgráf egy körvonal mentén elhelyezkedő pontok összekötésével készült ciklikus gráf. A pontok száma minimálisan kettő lehet, de a gyakorlatban praktikusnak láttam négy ponttal kezdeni a modellezést, mivel a két és három pontból álló körgráfnak csak egy-egy változata (formája) lehetséges. Az összekötő élek a beágyazási környezetül szolgáló síkban egyenes szakaszok, amik kialakítása (megrajzolása) során több szabályt alkalmaztam a lehetőségek leszűkítése érdekében.
Első szabály: A körvonalon lévő, egymással szomszédos pontok távolsága csak egyforma lehet. Vagyis a pontok annyi egyenlő részre osztják a körvonalat, ahányan vannak.
Második szabály: Az élek húzása mindig a legfelső ponttól kezdődik, az egyszerűség érdekében.
Harmadik szabály: Minden él az előzőleg meghúzott él végpontjából indul. Vagyis az élek együttese egy utat alkot. A csúcspontok lehetnek ismétlődőek, az élek nem. Az élek metszhetik egymást a síkban.
Negyedik szabály: Az élek irányítottak (ezt a rajzokon nem jelöltem), körbejárásuk a gráfon egyirányú és jobbos, vagyis órairányban történik az egyszerűség kedvéért. Irányváltás nem engedélyezett.
Ötödik szabály: Az utolsó él végpontjának azonosnak kell lennie az első él kezdőpontjával, hogy teljes legyen a ciklus. Vagyis a pontokból kivezető élek száma (a fokszám) minimum kettő kell legyen. Izolált csúcsok (fokszám: nulla) engedélyezettek, vakvágány (fokszám: egy) nem engedélyezett. A körgráf ezért lehet reguláris (minden csúcs fokszáma azonos) vagy nem reguláris.
Hatodik szabály: Amennyiben a körgráf szimmetriája megkívánja, a kezdőpont elérése után is tovább folytatható az élek hozzáadása (csak többféle értékű lépésszám esetén), míg újra a kezdőponthoz nem érünk. Az élek hozzáadása leáll akkor, ha a folytatás párhuzamos éleket eredményezne. Tehát két pont között két él nem engedélyezett. A hurokél (egy pontot önmagával összekötő él) szintén nem engedélyezett.
Hetedik szabály: A kimaradó pontok maradhatnak életlenek vagy belőlük új körgráf indítható. Ekkor mindig a kezdőponttól jobbra eső első izolált pont lesz az új kezdőpont.
Nyolcadik szabály: Az él húzását meghatározó lépésszám (L) értéke a körgráf pontjainak számához (P) képest maximum kevesebb, mint feleakkora lehet. Ha ugyanis L=P/2, akkor egy P/2 szakaszból álló, P csúcsú (sugaras) csillagot kapunk, ha pedig L>P/2, akkor az él húzási iránya a körben irányváltásként is értelmezhető. Tehát ha P páros szám, akkor 1=<L=<(P/2)-1. Ha P páratlan szám, akkor 1=<L=<(P-1)/2. Kivételt képez ez alól a négy pontú körgráf, ahol szükségesnek láttam az L=P/2-t is, a szakrális geometria megjelenítése érdekében.
Kilencedik szabály: A lépésszám értéke (és ezzel az élek hossza) lehet állandó (egyféle) vagy változó (többféle). A gyakorlatban azonban a változó lépésszámú lehetőségek közül csak a kétféle értékűekkel foglalkoztam az egyszerűség érdekében. Kivétel ez alól a 13 pontból álló körgráf rajza, ahol kíváncsiságképpen kipróbáltam néhány háromféle értékű lépésszámot is. A kétféle lépésszám alkalmazását az indokolta, hogy az energiakvantumok tachion forrásainak felvillanási sorrendje is kétféle lehet (a síkban és térben egyaránt) és kíváncsi voltam az eredményre.
Tizedik szabály: Az egyes körgráfok megnevezése a három jellemző paraméterük alapján történik. Ezek: az alkotó pontok száma (P), a lépések száma (L) és a körbejárás során megtett körök száma (K). Amennyiben a körgráf több, független hurokból áll, amiknek nincs közös csúcsuk, de az éleik metszhetik egymást, akkor mindegyik K értéke külön kerül feltüntetésre. Az összefoglaló táblázatban azonban (matematikai okokból) csak ezek összege szerepel. Egyes szabályos körgráfok emellett külön neveket is kaptak, hogy könnyebb legyen beszélni róluk. Ezek nyelvészeti titkaival a következő fejezetben foglalkozom.

3. NYELVÉSZETI ÉRDEKESSÉGEK

A különféle szerkezetű körgráfok között természetesen számos közismert ábra akad. Ezek a világ számos pontján ősidők óta használatos, szakrális, illetve misztikus szimbólumok, amik eredeti, ezoterikus jelentése mára sajnos kiveszett a köztudatból. Most azonban, a készítésükhöz vezető matematikai szabályok vizsgálata révén újra lehetősége nyílik az emberiségnek megismernie őket. Mindez nem volna lehetséges az elmúlt évtizedek egyre kiterjedtebb teremtésfilozófiai kutatásai nélkül, amikben komoly szerep jut a magyar nyelv titkos jelentéstartalmát elemző kutatóknak is. Az alábbiakban ezért röviden ismertetem a fontosabb, szabályos körgráfok nevével kapcsolatos izgalmas tudnivalókat.
A P=4, L=2, K=1, 1 körgráf közismert neve világkerék, sorskerék, szerencsekerék, ami egy körbezárt vízkeresztnek felel meg. Ez az asztrológiában a Föld szimbóluma, lásd: A keresztek titka (2010) című írást az Eseményhorizonton.
A P=5, L=2, K=2 körgráf közismert neve ötágú csillag, pentagramma vagy Püthagorasz-csillag, a Mindenható Isten monász térszeránjának síkvetületi szimbóluma, ami az időhurokban egymást kergető tachion forrásokat jelképezi.
A P=6, L=2, K=1, 1 körgráf közismert neve hatágú csillag, hexagramma vagy Dávid-csillag, a Mindenható Isten monász térszeránjának síkvetületi szimbóluma, ami az időhurokban keletkező tachion forráshelyeket (az öt tachiont és az üresen maradó nemtér-nemidő réteget) jelképezi.
A P=6, L=1-3, K=2 körgráf közismert neve tércsillag, ami a valknut egy speciális, de szabályos változata. Ez a Mindenható Isten monász térszeránjának síkvetületi szimbóluma (3D-ből vetítve), ami az időhurokban egymást követő tachion források felvillanási sorrendjét, körbejárási útvonalát jelképezi.
A P=7, L=2, K=2 körgráf közismert neve hétágú csillag vagy heptagramma, amit a pentagramma és a hexagramma mellett sheriff csillagként használnak manapság. Ez a monád fotinó fényszeránjának síkvetületi szimbóluma, ami az időhurokban egymást kergető tachion forrásokat jelképezi.
A P=8, L=2, K=1, 1 körgráf közismert neve nyolcágú csillag, ami gyakori ábrázolás a misztikában és az iszlám művészetben. Ez azonban nem a fotinó, hanem a Bindu szimbóluma az időfizikában, lásd a Szalagológia (2004) című kutatási anyagot az Eseményhorizonton.
A P=8, L=3, K=3 körgráf közismert neve oktagramma, nyolcágú csillag vagy fénycsillag, ami gyakori ábrázolás a misztikában és több vallásban. Ez a monád fotinó fényszeránjának síkvetületi szimbóluma, ami az időhurokban egymást követő tachion források felvillanási sorrendjét, körbejárási útvonalát jelképezi.
A P=9, L=2-4, K=2 körgráf közismert neve valknut, Hrungnir szíve vagy Odin-csomó, ami a skandináv mitológia egyik legősibb, ma is használt szimbóluma. Ez a tércsillaghoz hasonlóan a Mindenható Isten monász térszeránjának síkvetületi szimbóluma (valószínűleg 4D-ből vetítve). Az egyetlen hurokból álló mellett használják a három egyenlő oldalú háromszögből összefont változatát is, ami azonban egész mást jelent, ezért matematikai szempontból pontatlannak tekintendő.
A valknut szó jelentése a történészek szerint „az elesett harcosok csomója”, magyarul azonban ez a vala-ká-n-út, azaz a Ká (Teremtő Atya tachion) hullámterének (vala: a van befejezett múlt ideje) útvonala (Nut egyiptomi égistennő nevéből). Vagyis a Teremtő tachion által az őskáoszban megtett útvonal jelképe. Még pontosabban a primer időszál (tűzvonal) szakaszán belül az első rangú időhurok (az Isten) tachionjainak pályagörbéje, ami a monász térszerán térdimenziószáma és korlátlan mozgása miatt 4D-s. Bár matematikailag még nem sikerült igazolnom, de a nyelvi és időfizikai logika alapján erősen gyanítom, hogy a valknut a 4D-ben forgolódó (csavarodó) monász szerinó tachionjainak felvillanási sorrendjét határozza meg, 2D-be vetítve. Akit izgat a kérdés, megpróbálhatja igazolni a sejtést és elküldheti az Eseményhorizontnak.
Az „elesett harcosok csomója” kifejezés csak annyiból találó, hogy az Isten időhurok csomója valóban elesik, azaz elsodródik, eltávolodik a Teremtő okforrásától a hullámtérben (ami meg az emanációnál gyorsabban száguld el tőle). A valknutot azért tekintik a harcosok csomójának, mert a mitológia szerint a szent ügyért meghalt (elesett) katonák lelke ide kerül (az Istenhez), a mennyországba.
A Hrungnir szíve kifejezést a mitológiában az Edda nevű szentiratból származtatják, amiben egy Hrungnir nevű harcos szívének keménységét és alakját hasonlítják a valknuthoz. A Hrungnir szót magyarul inkább három-gir-nek kellene mondani, azaz három szívnek (a gir a sumerben szív, korona, út, tőr jelentésű), mivel jelképe három háromszög összekapcsolásával jön létre.
Az Odin-csomó a skandináv mitológia főistenének, Odinnak a jelképe, akit az összes Ász-isten apjának tartanak (helyesen). Odin neve magyarul ó-élő (a din a sumerben élni jelentésű, dingir alakban istent, isteneket jelent), vagyis Öreg Élő Isten. Innen származik az angol ten (ejtsd: tín), azaz tíz számnév is, ami utal a térszeránt létrehozó tíz okforrásra, akik hullámterében az időhurok keletkezett és működik. Természetesen a valknut szóból ered az angol knot (csomó) kifejezés is.
A P=12, L=1-5, K=1, 1, 1 körgráf közismert neve az élet csillaga (hatágú csillag), ami számos országban a mentőszolgálatok és sürgősségi orvosi szolgálatok szimbóluma (benne egy caduceus-szal). Az élet csillagával kapcsolatos további tudnivalókat lásd: A pásztorbot titka (2009) című írásban az Eseményhorizonton.

4. A 4 PONTÚ KÖRGRÁF

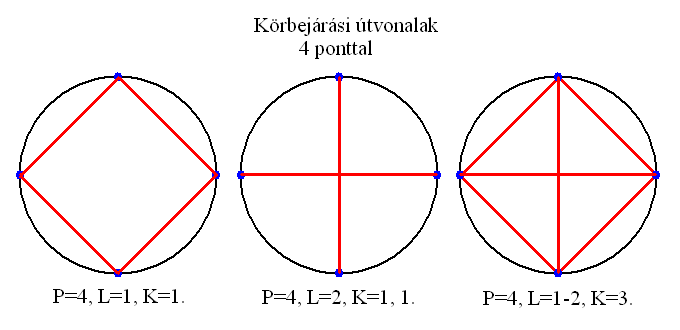
Négy pont esetén nem sok lehetőség adódik az összekötésükre. Az egyik négyzetet eredményez, a másik világkereket. Az L=1-2 esetén a kettő kombinációja alakul ki, ami annyiból különleges, hogy a négyzet átlói dupla élek lesznek, méghozzá ellenkező irányúak.
A pontok szögtávolsága az origóból nézve 90 fok.


5. AZ 5 PONTÚ KÖRGRÁF

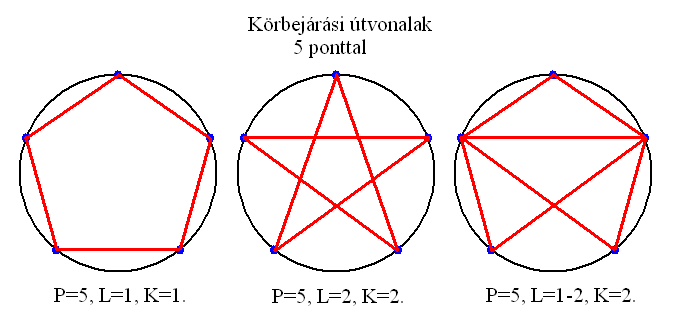
Öt pont összekötésével 3 szerkezet hozható létre. Egy szabályos ötszög, egy pentagramma és egy szabálytalan geometria. Mivel az élek metszik egymást a síkban, a pentagramma forgásiránya csak irányított élek használatával értelmezhető.
A pontok szögtávolsága az origóból nézve 72 fok.


6. A 6 PONTÚ KÖRGRÁF

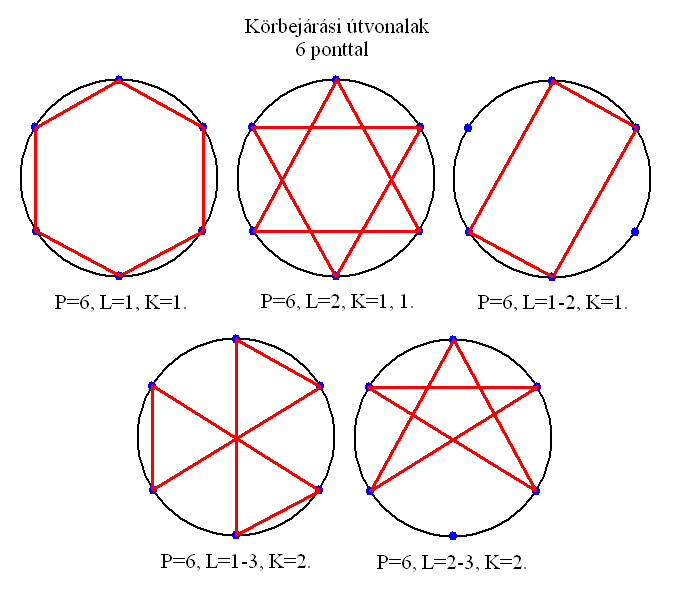
Hat pont összekötésekor 5-féle alakzatot sikerült létrehoznom. Az első a szabályos hatszög, a második a hatágú csillag, a harmadik egy téglalap, a negyedik a tércsillag, az ötödik pedig egy szabálytalan pentagramma.
Az L=1-2, K=1 körgráf egy olyan téglalapot ad, aminek a rövidebb oldala a kör sugarával egyenlő, a hosszabb oldal hossza pedig ennek gyök háromszorosa.
A pontok szögtávolsága az origóból nézve 60 fok.


7. A 7 PONTÚ KÖRGRÁF

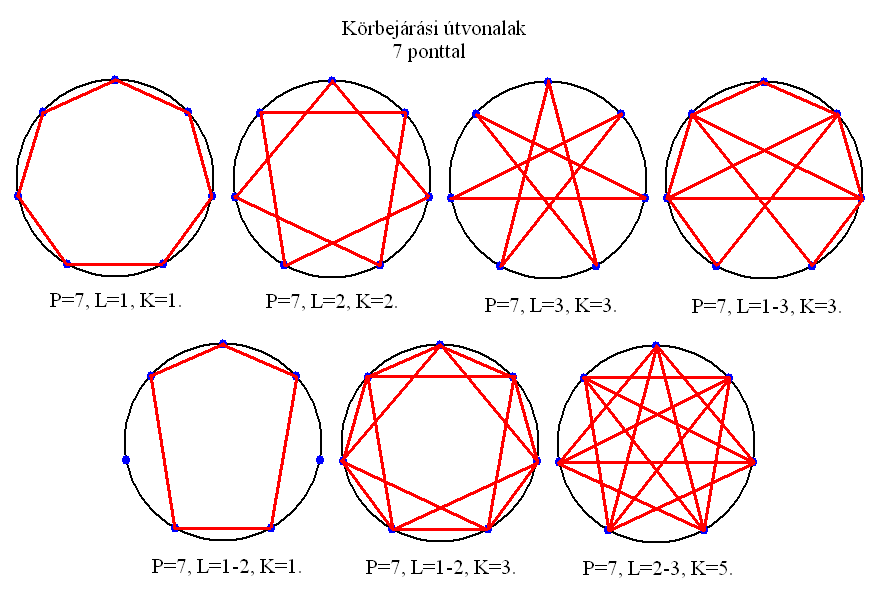
A hét pontú körgráfnak 6 verziója van. A szabályos hétszög mellett megjelenik egy szabálytalan alakzat, valamint a kis csúcsú és nagy csúcsú hétágú csillagok egyszerű (két száras) és kiegészített (négy száras) változata. A kis csúcsú csillag négy száras változata hétszögbe van írva, a nagy csúcsú csillagé pedig egy kis csúcsúval van kombinálva.
A pontok szögtávolsága az origóból nézve 51,42 fok.


8. A 8 PONTÚ KÖRGRÁF

Nyolc pont esetén 8 lehetőség adódik. A szabályos nyolcszög mellett a nyolcágú csillag, a fénycsillag egyszerű, és nyolcágú sugaras csillaggal kiegészített változata, valamint egy vaskos vízkereszt (L=1-3, K=1, 1) és három szabálytalan alakzat. Érdekes tény, hogy csak a hét és nyolc pontú körgráfoknál lesz azonos a pontok és lépési lehetőségek száma. Ez alatt kevesebb (P>L), fölötte több (P<L) lehetőség adódik a szabályok korlátozásai miatt.
A pontok szögtávolsága az origóból nézve 45 fok.


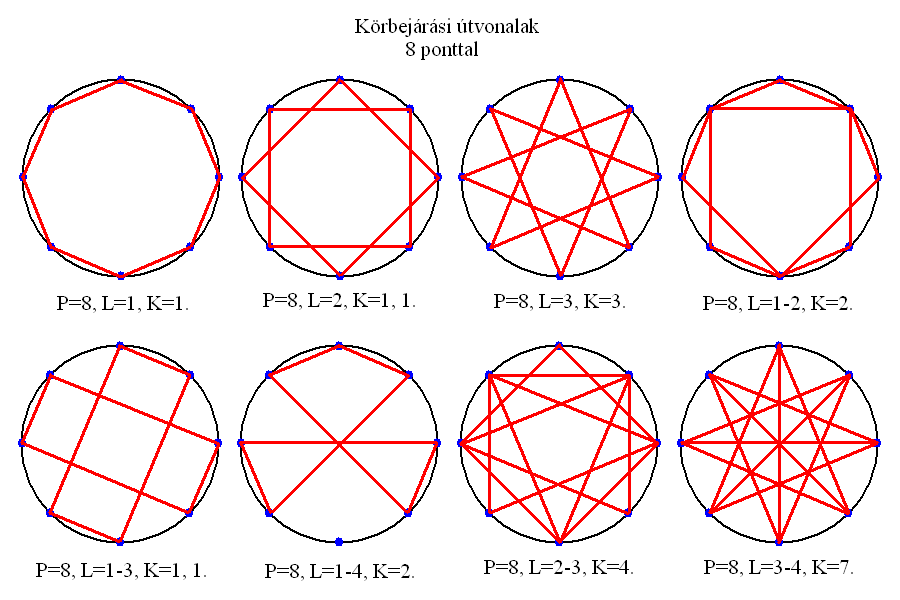
9. A 9 PONTÚ KÖRGRÁF

Kilenc pont összekötésekor a 10 lehetőség közt három különféle kilenc csúcsú csillag is kialakul, attól függően, hogy a lépések száma 2, 3 vagy 4. Megjelenik továbbá a valknut (L=2-4, K=2), és a négy szabálytalan alakzat mellett egy félszabályos hatszög, ami leginkább egy levágott csúcsú szabályos háromszögre hasonlít.
A pontok szögtávolsága az origóból nézve 40 fok.


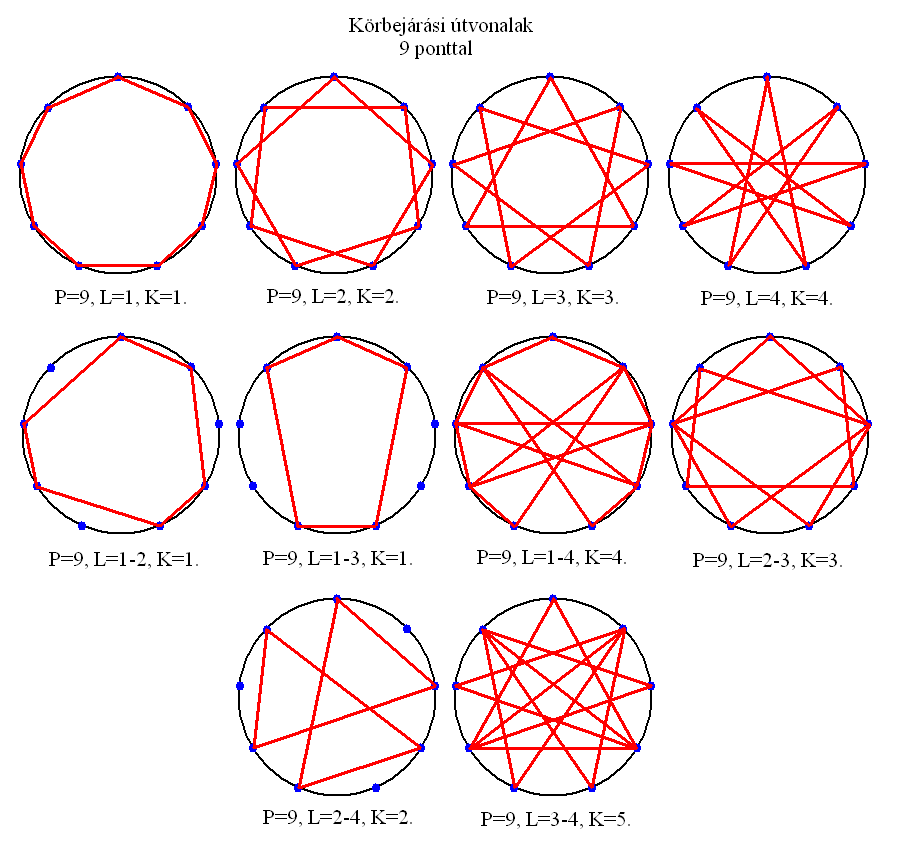
10. A 10 PONTÚ KÖRGRÁF

Tíz pont esetén szintén 10 lehetőség adódik. Itt a tíz csúcsú csillagok közül csak az L=3 lesz egységes. Az L=2 valójában két egymásba helyezett (és egymáshoz képest 36 fokkal elfordított) ötszögből, az L=4 pedig két egymásba helyezett pentagrammából áll.
Az L=1-3, K=2 alakzat egy levágott csúcsú pentagrammára hasonlít, az L=2-4, K=3 körgráf pedig egy ötszögbe rajzolt pentagramma lesz. Az L=3-4, K=7 formáció szintén szabályos alakzat, egy olyan tíz csúcsú csillag, aminek minden csúcsa négy szárral (éllel) rendelkezik.
A pontok szögtávolsága az origóból nézve 36 fok.


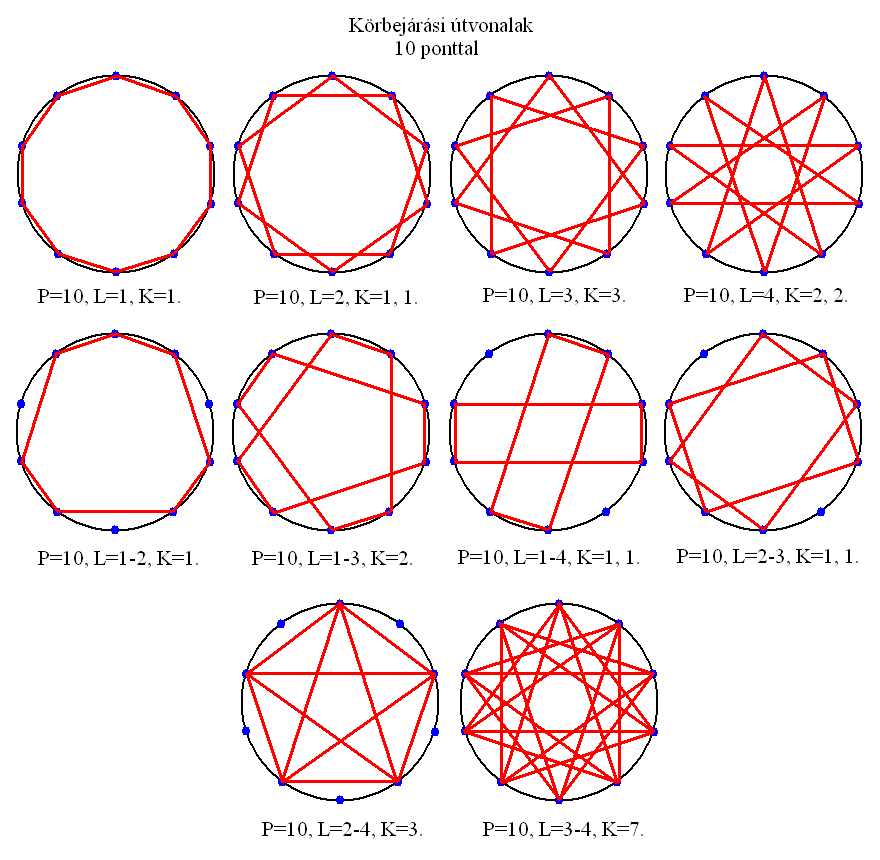
11. A 11 PONTÚ KÖRGRÁF

A tizenegy pontú körgráf 16 lehetőséget kínál a rajzolgatásra. A 2, 3, 4 és 5 lépéses, tizenegy csúcsú csillagok mellett mindegyiknek elkészíthető a tizenegyszögbe írt változata is, amennyiben a lépések száma 1-2, 1-3, 1-4 és 1-5. Ezekből csak az L=1-4, K=5 változatot rajzoltam meg. Az L=4-5, K=2 egy szabálytalan pentagrammát ad, amit tovább rajzolva K=9-nél egy szabályos, tizenegy csúcsú csillagot kapunk, minden csúcsán négy szárral.
A pontok szögtávolsága az origóból nézve 32,72 fok.


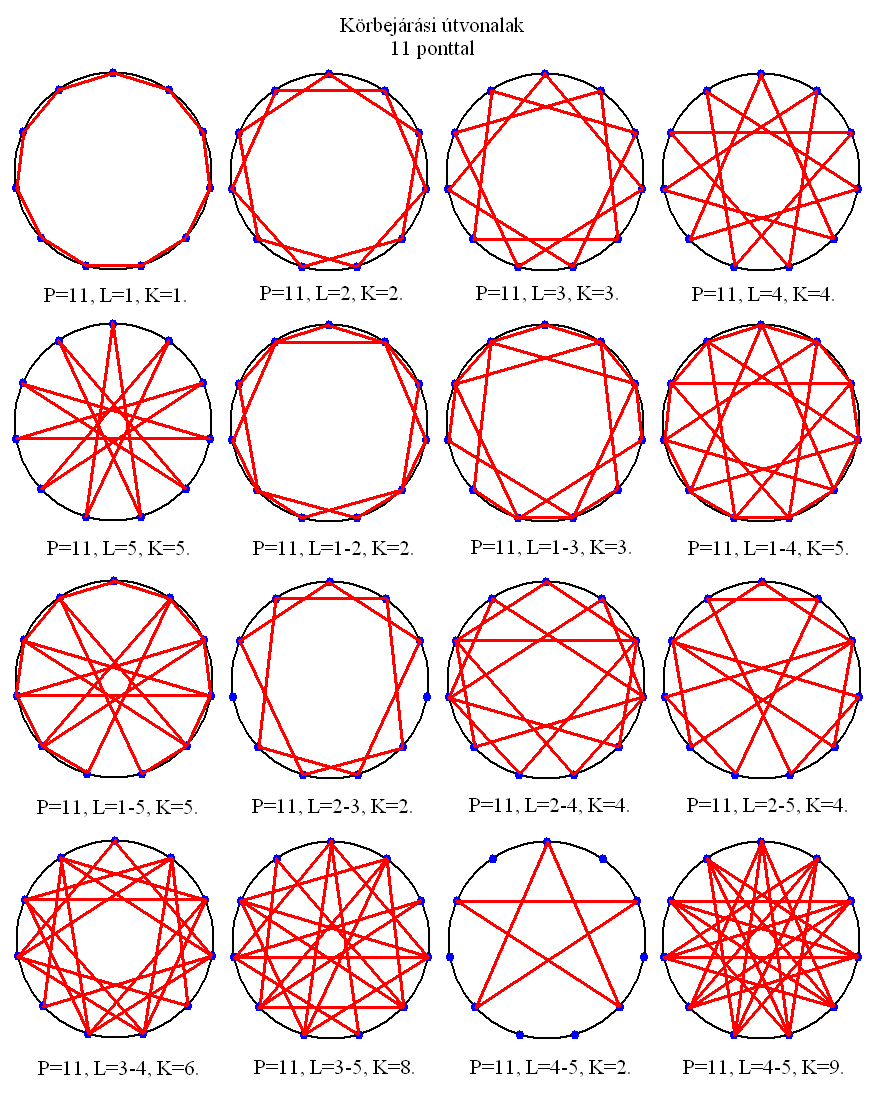
12. A 12 PONTÚ KÖRGRÁF

Tizenkét pont esetén szintén 16 lehetőség adódik. Az L=2, K=1, 1 két szabályos hatszögből áll, az L=3, K=1, 1, 1 három négyzetből, az L=4, K=1, 1, 1, 1 pedig négy szabályos háromszögből. Ezek mellett látható továbbá levágott sarkú négyzet, levágott csúcsú szabályos háromszög, négyszögletes csúcsú hatágú csillag, valknut, fénycsillag és két küllős kerék formájú csillag (az L=2-3, K=5 és az L=3-4, K=7).
A pontok szögtávolsága az origóból nézve 30 fok.


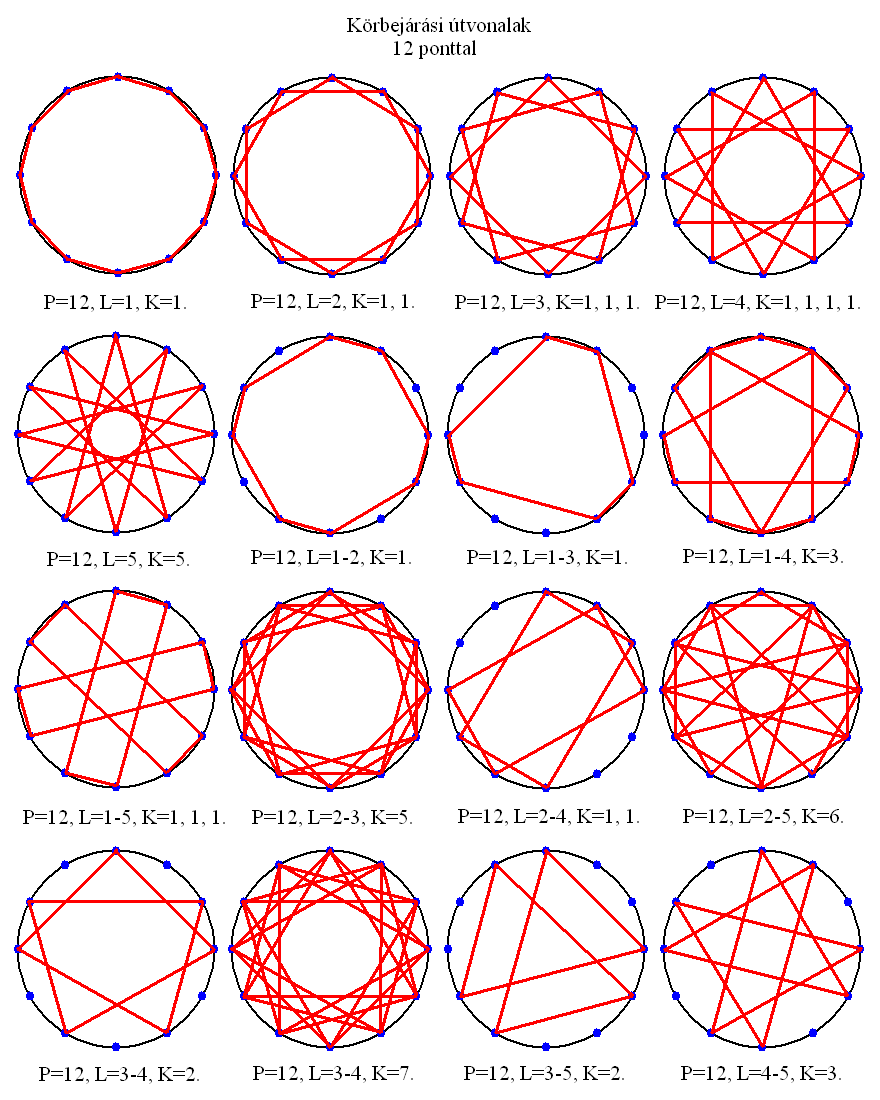
13. A 13 PONTÚ KÖRGRÁF

Tizenhárom pont esetén a 2, 3, 4, 5 és 6 lépéses tizenhárom csúcsú csillagok mindegyike egységes alakzat lesz, amik tizenháromszögbe zárt változatai egyaránt kialakíthatók az 1-2, 1-3, 1-4, 1-5 és 1-6 lépés kombinációkkal (csak az 1-5 és 1-6-ot csináltam meg). Az összes többi lehetőség szabályos vagy szabálytalan körgráfokat eredményez. Ennek valószínűleg az az oka, hogy a 13 prímszám, így a legtöbb lépésszám csak sok körbejárás után ér vissza a kiindulási pontra. Ugyanez természetesen megfigyelhető a többi prímszám esetén is (5, 7, 11).
Mivel egyes lehetőségek (itt és a továbbiakban) nagyon bonyolult formákat eredményeztek, egészséges lustaságból mellőztem ezek K értékének megállapítását. Aki kíváncsi rájuk, számoljon utána. A 21 lehetséges alakzat mellett érdekességképpen megrajzoltam három olyat is, ahol háromféle lépés kombinálódik, de ezek nem adtak szabályos formákat.
A pontok szögtávolsága az origóból nézve 27,69 fok.


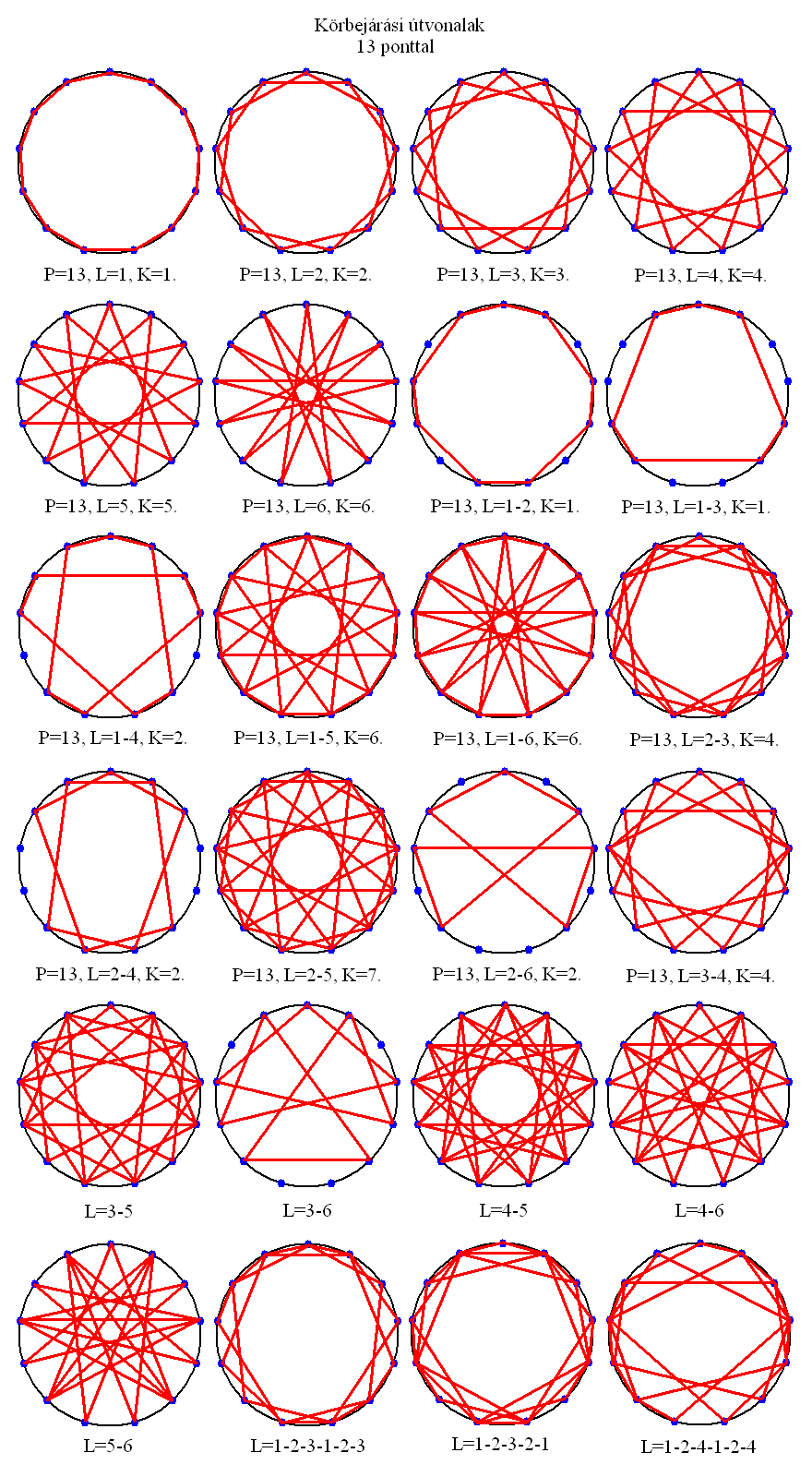
14. A 14 PONTÚ KÖRGRÁF

A tizennégy pontú körgráf szintén 21 lehetőséget kínál (az L=1, K=1-et nem ábrázoltam, mert alig különbözik a körtől). Köztük az egy lépéses csillagok mind egységesek, és különlegességük, hogy az L=4, K=2 csak hétágú, kis csúcsú csillagot ad, míg az L=6, K=3 egy nagy csúcsú, hétágú csillag lesz. Ezek sokszögbe zárt változatai is elkészíthetők értelemszerűen a lépések kombinálásával.
A sokféle formáció közül kiemelkedik az L=3-5, K=4 geometria a szabályosságával és szépségével, ami akár egy tibeti mandalában is megállná a helyét, bár ilyen szimmetriát nem szoktak készíteni, mert nem tükrözi a teremtés valamely ismert megnyilvánulását. A mandalák között egyébként ritka a hetes szimmetria ábrázolása, de ez az ábra nem a diád fotinó szimbóluma (ha esetleg valaki erre gyanakodna), mert nem kétszer hét, hanem egyszer tizennégy csúcsú ciklust alkot.
A pontok szögtávolsága az origóból nézve 25,71 fok.


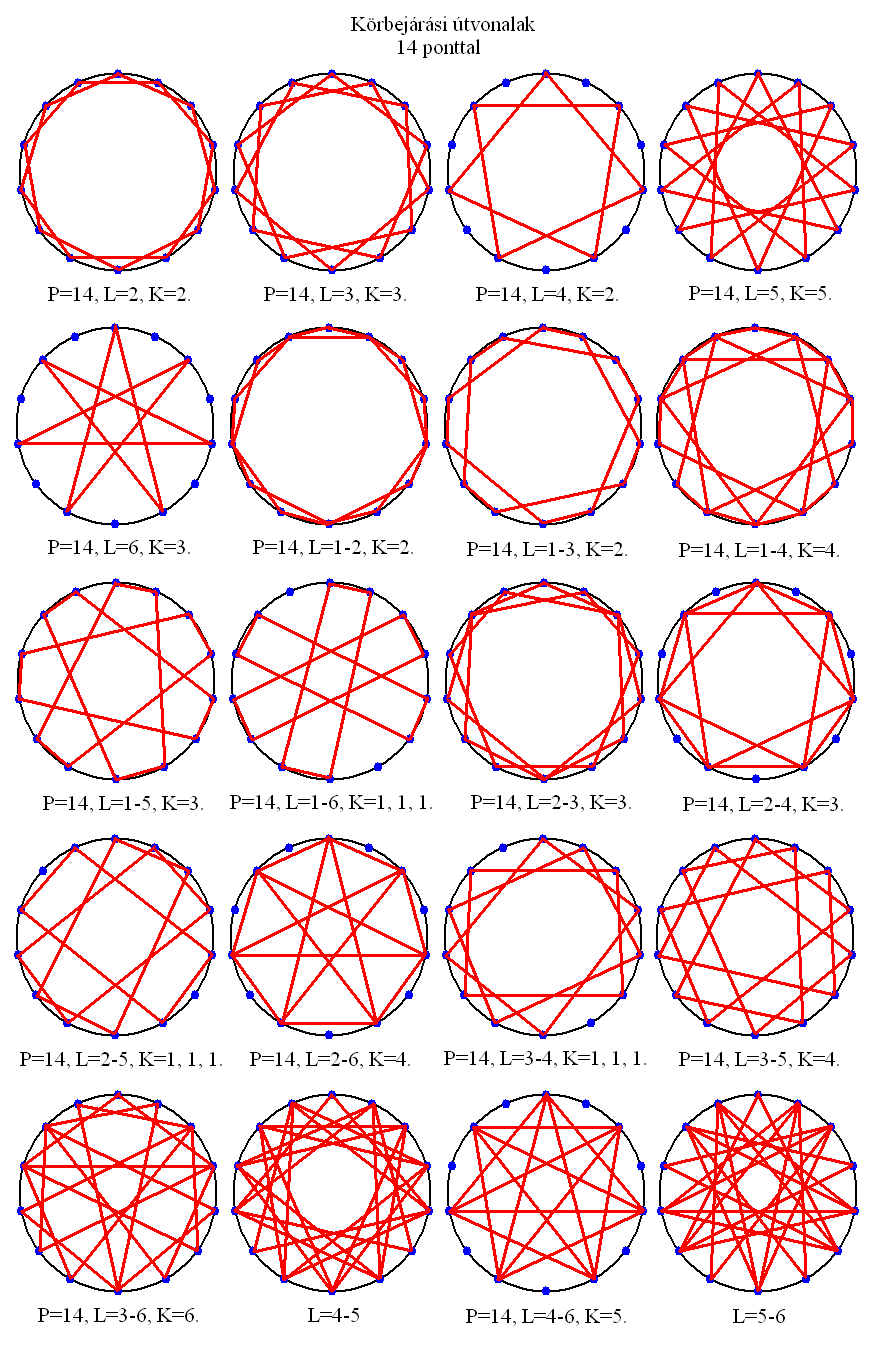
15. A 15 PONTÚ KÖRGRÁF

Tizenöt pont esetén a lehetőségek száma 28. A sokcsúcsú csillagok egyre inkább kezdenek küllős kerekekre hasonlítani. Itt is megjelenik az ötszögbe rajzolt pentagramma, a levágott csúcsú pentagramma két változata, a valknut két változata, a szabálytalan hétágú, nagy csúcsú csillag és különféle további szimmetriák, amik közül a legérdekesebbek az L=2-7, K=3 (ami a lovag kereszt ötszárú változatára hasonlít, közepén egy pentagrammával) és az L=5-7, K=4 (ami egy kis pentagramma köré illesztett öt nagy pentagrammát formáz, és egyben tízágú, speciális csillag is). Ez utóbbi kettő szintén tibeti mandalába való szépségű, bár nem találtam akár csak hasonló formációkat sem az interneten (annak ellenére, hogy mindkettő szakrális jelentőségű). Az L=2-7, K=3 alakzat a téridő öt téresszenciáját, a kvintesszenciát szimbolizálja, míg az L=5-7, K=4 az alfatéri szerinóból leágazó öt bétatéri szerinó születését jelképezi (a Mindenhatót és öt arkangyalát).
A pontok szögtávolsága az origóból nézve 24 fok.


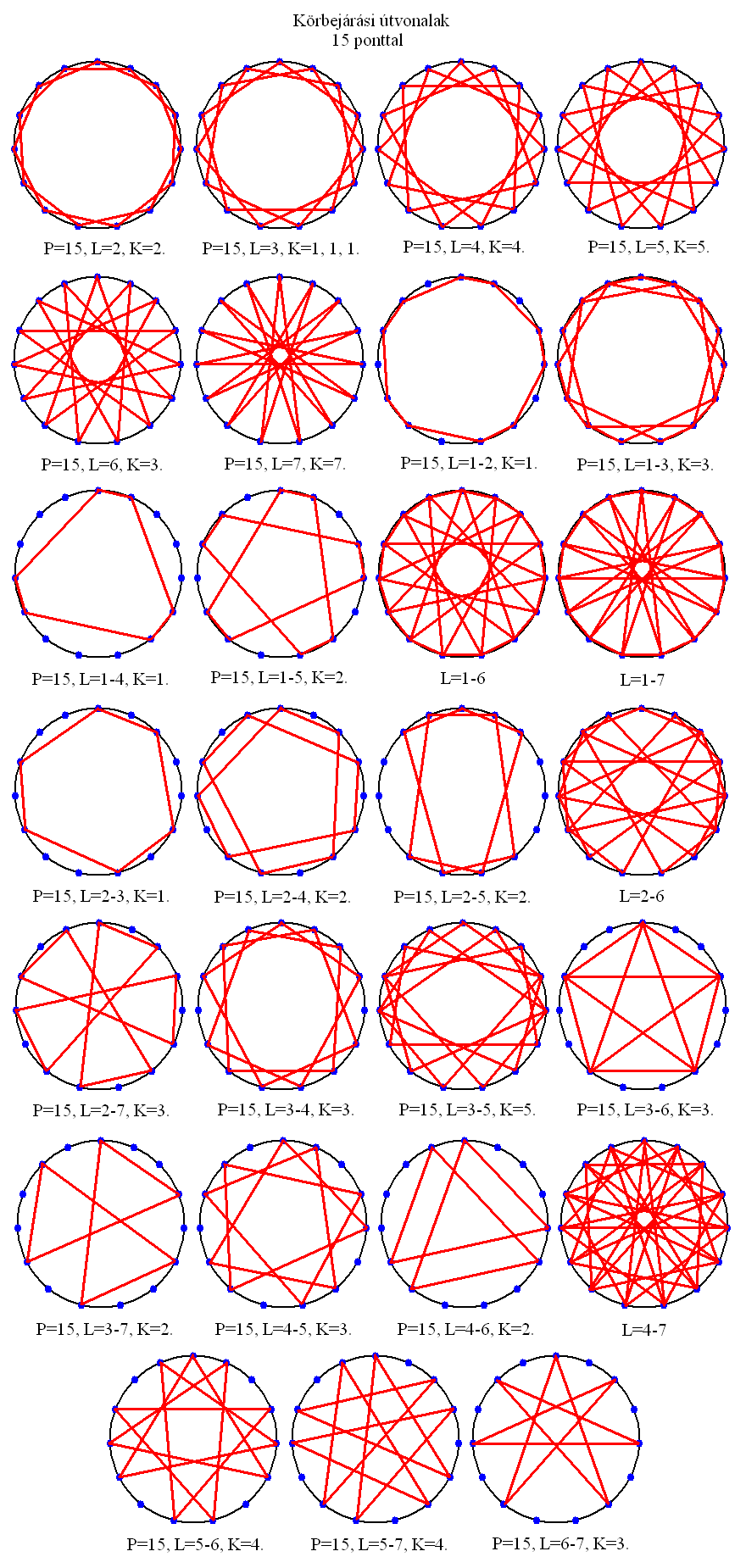
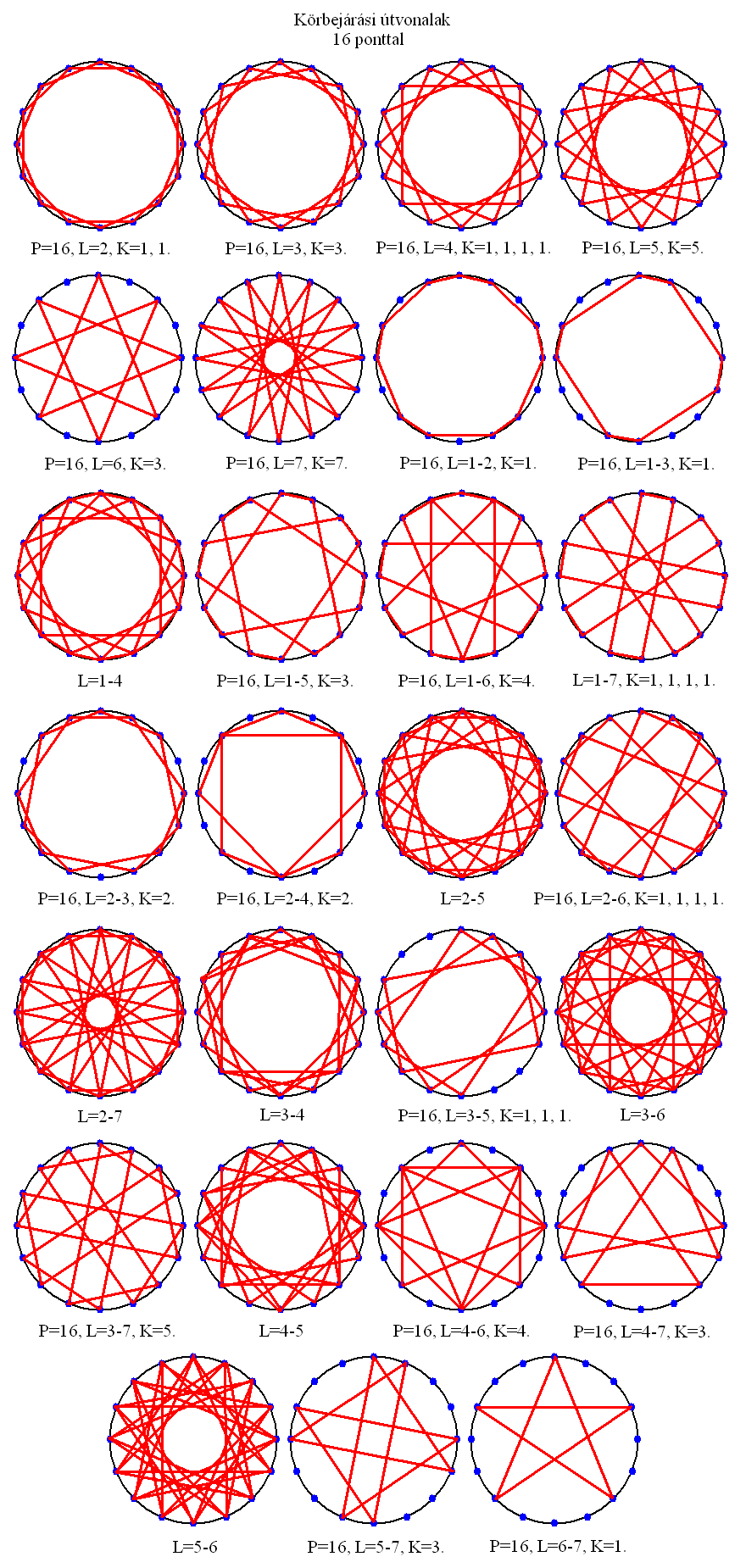
16. A 16 PONTÚ KÖRGRÁF

A tizenhat pontú körgráf volt az utolsó, aminek megrajzolására még el tudtam szánni magam. Főként azért, hogy igazoljam a fénycsillag megjelenését előrejelző képletet (lásd a 18. fejezetben), mivel a 16 néggyel osztható. Ezekből is 28-féle készíthető egyébként és a szabályos alakzatok egyre bonyolultabbá válnak, a korábban megismert szabályok szerint. Tehát az L=2, K=1, 1 körgráf két szabályos nyolcszögből áll, az L=4, K=1, 1, 1, 1 pedig négy négyzetből. Az egy lépéses csillagok sokszögbe zárt változatai is elkészíthetők megfelelő lépés kombinációkkal, mint például az L=1-4 alakzat. Fénycsillagot eredményeznek az L=6, K=3 és az L=5-7, K=3 alakzatok, amik mellett megjelennek különféle szabálytalan fénycsillagszerűségek is (levágott csúcsú, szögletes végű, kettős csúcsú). Az L=6-7, K=1 formáció szabálytalan pentagrammát ad, ami azért érdekes, mert a szabálytalan pentagramma mindig azoknál a köröknél jelenik meg, ahol a pontok száma öt egész számú többszöröse, plusz egy.
Az L=5-7, K=3 geometria kapcsán felmerült bennem a lehetőség, hogy ennek a szabályos, mégis torz fénycsillagnak esetleg köze lehet a 4D-s fotinóhoz. Ahogyan a P=6, L=1-3, K=2 tércsillag a 3D-ben másodlagos csavarodásokat végző szerinó síkvetülete, míg a P=9, L=2-4, K=2 valknut a 4D-ben harmadlagos csavarodásokat végző szerinó síkvetülete, ugyanúgy a fény esetében is léteznie kell a körgráf rendszerben mindkét változatnak. Sejtésem az, hogy míg a P=8, L=3, K=3 fénycsillag (vagy a P=16, L=6, K=3) a 3D-ben csavarodó fotinó (kocka) síkvetülete, addig a P=16, L=5-7, K=3 fénycsillag (vagy a P=12, L=4-5, K=3) a 4D-ben csavarodó fotinó (hiperoktaéder) síkvetülete lehet. Ha valakinek sikerült matematikailag igazolnia a dolgot, kérem küldje el az Eseményhorizontnak a levezetést.
A pontok szögtávolsága az origóból nézve 22,5 fok.


17. A MEGTETT KÖRÖK SZÁMÁNAK TÁBLÁZATA

Miután megrajzoltam a különféle körgráfokat, készítettem belőlük egy táblázatot, hogy átlátható legyen a legfontosabb paraméterük változása. Ez pedig a körbejárás során megtett egész körök száma, ami arról árulkodik, hány fordulat után kerül vissza a rendszer a kiindulási állapotába. Az öt, hat, hét és nyolc csúcsú változatokat színessel kiemeltem, ami rögtön elárulja a pontok száma és csúcsok száma közti összefüggéseket.


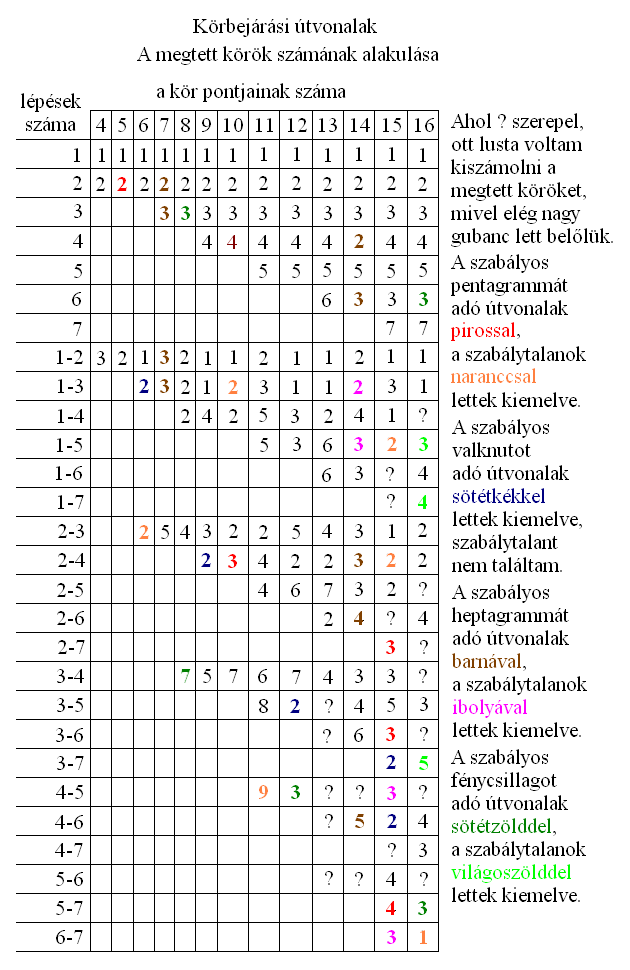
18. SZÁMTANI SOROZATOK

A megtett körök számának táblázata alapján azonnal feltűnik, hogy a nevezetes alakzatok megjelenése számtani sorozattal leírható szabályokat követ. Ezeket foglaltam össze az alábbi képen.


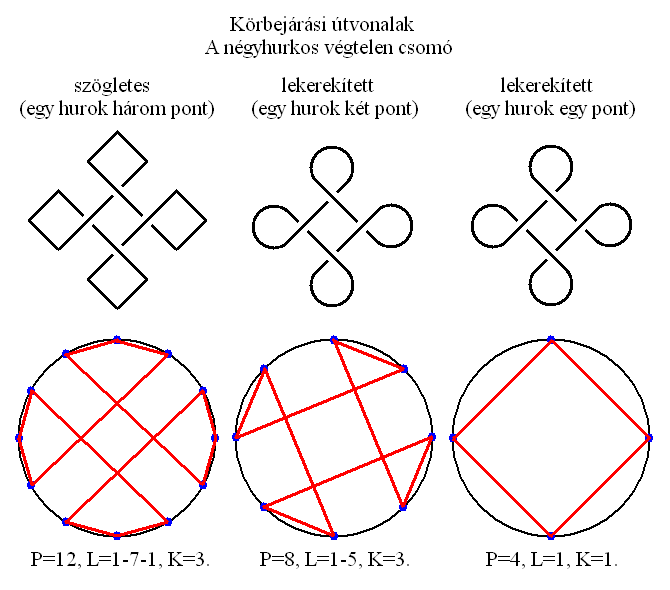
19. A VÉGTELEN CSOMÓK

Az Odin-csomó vizsgálatától ihletet kapva megvizsgáltam két másik közismert, ősi ábrát is, a négyhurkú és hathurkú végtelen csomókat, amiket minden kultúrában az örök élettel társítanak a misztikusok. A négyhurkú végtelen csomót hívják négyhurkú keresztnek is (részletesen lásd: A keresztek titka című publikációban), míg a hathurkút szerencse csomónak (pan-zhang). A hathurkú csomó a buddhizmus nyolc szent jelképe közül az egyik, ami a hindu mitológia szerint Visnu mellkasát díszítette eredetileg és máig elterjedt jelképnek számít Kínában és Tibetben. A végtelen csomóknak (mert vannak több hurkú, bonyolultabb változatai is) két változata használatos. Az egyik a szögletes, a másik a lekerekített kialakítású. A négyhurkú végtelen csomó szalagja négyszer, a hathurkú pedig kilencszer lapolja át önmagát a térben (2x2-es, illetve 3x3-as szimmetriában). Ezeket a szimbólumokat kétféleképp lehet körgráffá alakítani attól függően, hogy a szögletes vagy lekerekített változatból indulunk ki.
A négyhurkú, szögletes csomó külső csúcsait kifeszítve egy körvonalra 12 pontú körgráfot kapunk. Ennél L=1-7-1, K=3. Ha levesszük a külső négy csúcsát és nyolc csúcsúvá redukáljuk az egyszerűség miatt, akkor a L=1-5, K=3 alakzatot kapjuk. A lekerekített csomó négy hurkát egy-egy pontnak tekintve a P=4, L=1, K=1 alakzatot kapjuk, ami egy körbe rajzolt négyzet lesz.


A hathurkú, szögletes csomó külső csúcsait kifeszítve egy körvonalra 14 pontú körgráfot kapunk. Ennél L=1-9-13-7-1-5-13-13-5-1-7-13-9-1, K=7. Ha redukáljuk a körgráfot 12 pontúra, hogy minden hurok két pontból álljon, akkor L=1-8-11-6-1-4-11-4-1-6-11-8-1, K=6. A lekerekített csomó hat hurkát egy-egy pontnak tekintve a P=6, L=2-3-4-4-3-2, K=3 formációt kapjuk, ami egy tengely szimmetrikus geometria lesz.


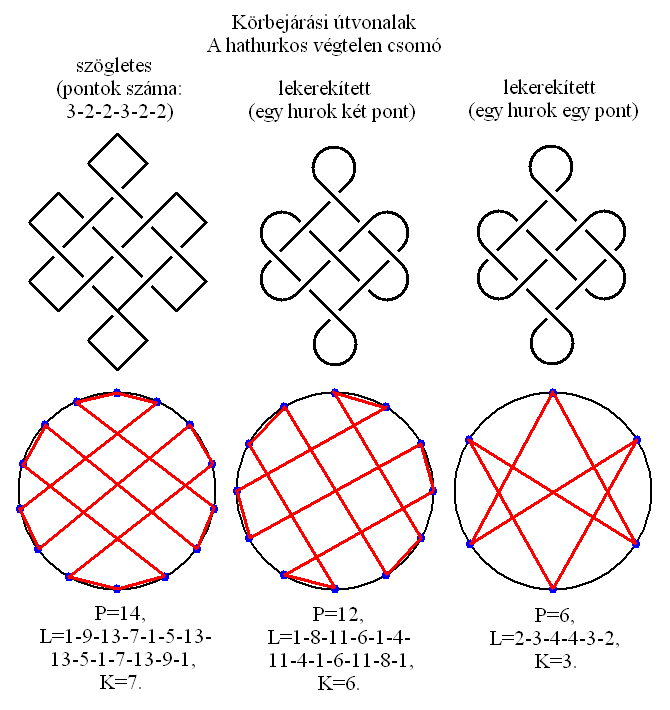
A mellékelt ábrákon látható, hogy egyik lehetőség sem tartozik a szűkebb értelemben vett körgráf rendszerbe. Persze ettől még van valamilyen kapcsolatuk a teremtéssel, de az egészen biztosan kijelenthető, hogy egyik sem valamely időhurok térbeli modellje, geometriai ábrázolása. A négyhurkú csomó a Bindu szimbólumával ekvivalens topológiailag, míg a hathurkú szerkezetileg rokonítható a szerinó időhurokkal, csak éppen pontatlan megjelenítése annak.

20. ÖSSZEFOGLALÁS

A szakrálisnak tekintett nevezetes ábrák kapcsolata a teremtés működésével egyértelmű és vitathatatlan, a feltárt matematikai összefüggések ismeretében. Az őseink valamikor régen tudták és értették a mögöttük rejlő időtlen bölcsességet, s bár ez a tudás az évezredek alatt majdnem teljesen elveszett, a szimbólumok mégis megmaradtak, hogy tanúskodjanak nekünk elődeink ismereteiről. Akik nem voltak primitív, tudatlan vademberek (vagy legalábbis nem mindenki), és mély, pontos információkkal rendelkeztek a világegyetem szerkezetéről és működésrendjéről.
Azt persze nem tudjuk, honnan vették a tudásukat, hisz a régészek (hivatalosan) még nem találtak ősi számítógépeket, részecske gyorsítókat és más technikai eszközöket az ásatások során. Vagy találtak, csak nem ismerték föl őket, esetleg eltitkolták a fölfedezést lányos zavarukban. A szakrális tudás akár egy előző, fejlett civilizációtól (Atlantisz?), akár idelátogató földönkívüliektől (szíriuszi űrhajósok?) vagy túlvilági szellemektől (istenektől?) származott, most mindenképpen hasznunkra válik, hiszen megerősíti saját teremtésfilozófiai kutatásainkat és segítséget nyújt a fogósabb fizikai, matematikai kérdések megfejtésénél.
Bárhol is legyetek most az univerzumban, okos elődeink, köszönjük nektek a megőrzött tudást és igyekezni fogunk tovább adni azt a következő generációknak. A lehető legpontosabban, kiszűrve belőle az évezredek során rárakódott esetleges hibákat és félreértéseket, illetve hozzátéve a saját fölfedezéseinket. Mert a tudást nem elég megőrizni és tovább adni. Használni és fejleszteni, bővíteni is kell, hogy a világ és az élet előrébb jusson a végtelenbe vezető, hosszú útján.

Készült: 2004.03.15. - 2010.07.19.

Következő írás

Vissza a tartalomhoz