KOCKA MANŐVEREK

Az űrhajók biztonságos mozgásához alapvető fontosságú a környezetükben lévő égitestek, más járművek helyének, távolságának, mozgási irányának és sebességének, egyszóval a mozgáspályáinak meghatározása, rendszeres nyomon követése és a velük való ütközések elkerülése. Minél nagyobb és fényesebb egy objektum, annál messzebbről látható. A radar csak a közeli, kisebb méretű objektumok észlelésére alkalmas, amik radarvisszhangja elfogadható időbeli késedelemmel, mérhető erősségű jelként tér vissza a mérőműszerhez.

A távoli, látható objektumok távolságának meghatározása parallaxis méréssel a legegyszerűbb. Ennek lényege, hogy két nézőpontból ugyanazon objektum máshol látszik a nagyon távoli objektumokhoz képest, amik nem mozdulnak el mérhető mértékben. Ha ismerjük a két nézőpont térbeli távolságát, egyszerű háromszög függvénnyel kiszámolhatjuk az objektum távolságát (nézőpontok távolsága osztva a látószög különbség tangensével).

Az egyenes pályán haladó űrhajók számára a legegyszerűbb parallaxis mérési módszer az, ha adott időközönként lefényképezik maguk körül az űrt és a látható objektumok elmozdulásaiból következtetnek a távolságukra. Csakhogy ez a módszer nem működik a haladási és érkezési irányba eső objektumoknál, amik látszólagos elmozdulása annál kisebb, minél közelebb esnek a pályavonalhoz. Így nehéz meghatározni, milyen messze van a hajó onnan, ahonnan elindult, illetve ahová igyekszik.

A hajótest mérete (legnagyobb keresztmetszete) meghatározza a burkolatán elhelyezhető mérőműszerek egymástól való távolságát a vizsgált irányokra merőlegesen, ami a mérési pontosság technikai korlátai miatt korlátozza a sikeres parallaxis mérés hatósugarát. Erre megoldást jelent, ha a mérőműszereket űrszondákra helyezzük és az űrhajó körül reptetjük, adott távolságra. A műszereket érdemes a szonda haladási irányára (X tengely) merőleges síkban (YZ sík), körben történő mérésekre beállítani. Mivel a parallaxis méréshez legalább két mérési pont kell és a köztük lévő szakasznak közel merőlegesnek kell lennie a mérendő pont irányához képest, logikus, hogy a mérőszondákat mozgatni kell az űrhajó körül ahhoz, hogy a teljes teret lefedjük velük körben. Az alábbiakban ezen mozgáspályák, mint "manőverek" kerülnek bemutatásra.

1. KOCKAFEJ MANŐVER

A kockafej manőver az űrhajó, mint fej körül az űrszonda által bejárt, kisebb kocka alakú útvonalról kapta nevét.

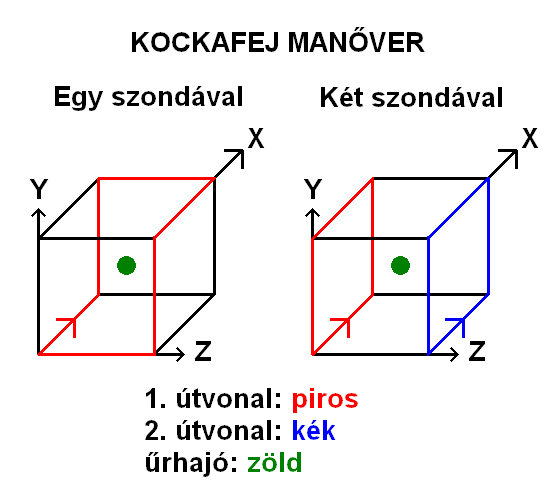
1.1. EGY SZONDÁVAL

Ha csak egy űrszondánk van a parallaxis mérésekhez, annak úgy kell végighaladnia egy képzeletbeli kocka élei mentén az űrhajó körül, hogy minden alkalommal a sarkokra érve úgy váltson irányt, hogy kilépjen az előző két élt tartalmazó síkból. Például: X tengely mentén előre, Y tengely mentén felfelé, Z tengely mentén jobbra, X tengely mentén hátra, Y tengely mentén lefelé, Z tengely mentén balra. Az űrhajó haladási iránya: X tengely mentén előre.

1.2. KÉT SZONDÁVAL

Ha két űrszondánk van, akkor a legegyszerűbb, ha egymással párhuzamosan mozognak egy kocka élei mentén, aminek a középpontjában az űrhajó található. Hátulról előre haladnak alul (X tengely), majd felfelé (Y tengely), aztán elölről hátra felül (X tengely), majd lefelé (Y tengely), vissza a kiindulási pontba. Az egymástól mért távolságuk közben nem változik. A műszereik így egyenként lefedik a haladási irányra (X tengely) merőleges síkot (YZ) kétszer körönként, illetve a vízszintes síkot (XZ) kétszer körönként, míg az előző kettőre merőleges síkot (XY) folyamatosan, ha a két szonda méréseit összevetjük.

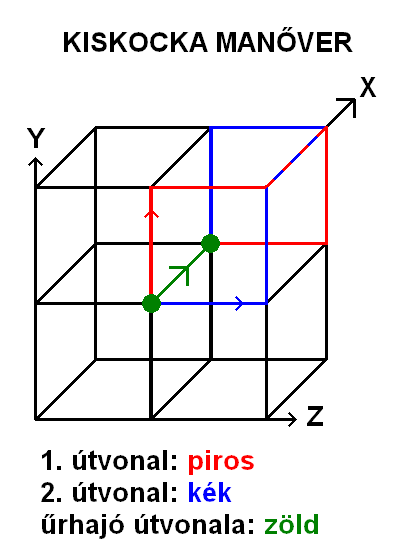
2. KISKOCKA MANŐVER

A kiskocka manőver az űrhajótól eltávolodó űrszonda által bejárt, kisebb kocka alakú útvonalról kapta nevét.

2.1. EGY SZONDÁVAL

Ha csak egy űrszondánk van a parallaxis mérésekhez, annak úgy kell végighaladnia egy képzeletbeli kocka élei mentén, elszakadva az űrhajótól, hogy a kocka egyik éle azonos legyen az űrhajó útvonalával. Ez összesen 4 kocka élei mentén, 8 féleképpen végrehajtható manővereket jelent, amiket alkalmanként lehet váltogatni is egymással, például adott irányban körbejárva a kockákat (jobb felső kocka, jobb alsó kocka, bal alsó kocka, bal felső kocka), illetve váltogatva a kockákban a kétféle bejárási útvonalat. Eközben az űrszonda minden alkalommal úgy vált irányt a kocka sarkaihoz érve, hogy kilép az előző két élt tartalmazó síkból. Az egy kockában bejárható két útvonal a következő a jobb felső kockában:
1. Y tengely mentén felfelé, Z tengely mentén jobbra, X tengely mentén előre, Y tengely mentén lefelé, Z tengely mentén balra.
2. Z tengely mentén jobbra, Y tengely mentén felfelé, X tengely mentén előre, Z tengely mentén balra, Y tengely mentén lefelé.
Az űrhajó haladási iránya: X tengely mentén előre. Az űrszonda haladási sebessége minden esetben ötszöröse kell legyen az űrhajóénak ahhoz, hogy újra találkozzon vele a kocka következő csúcspontjában az X tengely mentén.

2.2. KÉT SZONDÁVAL

Ha két űrszondánk van, akkor a legegyszerűbb, ha egymással ellentétes irányba mozognak, két élével szomszédos kocka élei mentén (például: 1. szonda: jobb felső kocka, 2. szonda: bal alsó kocka), vagyis a mozgáspályáik azonosak, csak 180 fokkal elforgatva. Körönként váltogathatják a bejárt kockákat az éggömb teljesebb lefedése érdekében (másodjára: 1. szonda: jobb alsó kocka, 2. szonda: bal felső kocka). A legnagyobb távolságuk egymástól ilyenkor a kocka élének négyzetgyök 5-szöröse.

3. NAGYKOCKA MANŐVER

A nagykocka manőver az űrhajó és az űrszonda által bejárt, a haladási útvonaltól rendszeresen eltérő, nagyobb kocka alakú útvonalról kapta nevét.

Ha nagyobb távolságra lévő égitestek parallaxisát akarjuk menet közben megmérni, akkor érdemes az egész űrhajóval irányt változtatni és egy nagyobb (sok milliárd kilométeres, akár több fényév élhosszúságú) kocka élei mentén repülni. Ez ugyan ötszörösére növeli a repülési útvonal hosszát, folyamatosan alkalmazva az indulási ponttól a célpontig, viszont ha az úthossznak és a repülési időnek nincs jelentősége (pl.: űrtérképezés esetén), lehetőséget ad a nagy pontosságú mérésekre. Erre azért van szükség, mert minél messzebbre küldi ki az űrhajó az űrszondáit, annál nagyobb a valószínűsége annak, hogy a navigációs pontatlanságok miatt elveszíti őket valamelyik nagykocka bejárása során. Vagyis a szonda nem talál vissza az űrhajóhoz és menthetetlenül eltéved a végtelenben. Nagykocka manőver során nincs szükség űrszondák kiküldésére, magáról az űrhajóról is lehet végezni a méréseket. Ez szintén 4 kocka élei mentén, 8 féleképpen végrehajtható manővereket jelent, amiket alkalmanként lehet váltogatni egymással, például adott irányban körbejárva őket (jobb felső kocka, jobb alsó kocka, bal alsó kocka, bal felső kocka).

4. DOBÓKOCKA MANŐVER

A dobókocka manőver az űrhajó és/vagy az űrszonda által térugrásokkal bejárt, különböző kocka alakú útvonalakról (kockafej, kiskocka, nagykocka) kapta nevét.

Ha nagyobb távolságra lévő égitestek parallaxisát akarjuk menet közben megmérni, de nincs türelmünk sokáig repülni az űrhajóval a térben, érdemes térugrásokkal lerövidíteni a kockák bejárási útvonalait. Ilyenkor az űrhajó vagy az űrszonda a kocka egyik csúcspontjától a másikig ugrik az élek mentén, majd a derékszögű forduló végrehajtása előtt és után is mér. A kocka élhosszúságát érdemes a térugrások optimális távolságának egész számú többszörösében meghatározni. Erre az esetre is érvényes az a szabály, hogy űrszondát kiküldeni csak kiskocka manőverben szabad, nehogy eltévedjen az ugrási pontatlanságok miatt.

Készült: 2021.09.25. - 30.

Következő írás

Vissza a tartalomhoz