SZOMSZÉDOS KÖRÖK SZÁMA N DIMENZIÓBAN
Az alábbiak megértéséhez érdemes elolvasni a következő cikket az Eseményhorizonton: Az n dimenziós kör definíciója (matematika, 2007). Ez a téma logikailag kapcsolódik még az alábbi 2007-es matematikai írásokhoz is: A hárompont tétel, Időtopológia, Merőlegesség n dimenzióban.
1. SZOMSZÉDOK
Kérdés: Az egységnyi átmérőjű, n dimenziós körnek hány, vele azonos átmérőjű, n dimenziós kör szomszédja lehet maximum, amikkel egy pontban érintkezik és amik egy pontban érintik egymást?
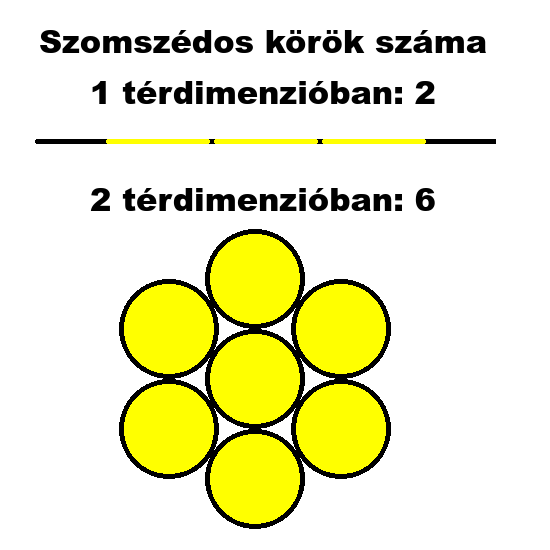

Ez a gömb pakolási probléma általános megfogalmazása, amikor egyforma méretű gömbökkel próbáljuk a lehető legjobban kitölteni a rendelkezésünkre álló teret. Mivel a választ ismerjük 1, 2 és 3 térdimenzióban, a számok alapján meghatározhatjuk a számtani sorozat képletét:
aˇn=(aˇn-1)+2xn
Ahol:
n: térdimenziószám (pozitív egész szám).
aˇn: a sorozat n. eleme szomszédainak száma n térdimenzióban.
Tehát:
0D-ben: 0
1D-ben: 0+2=2
2D-ben: 0+2+4=6
3D-ben: 0+2+4+6=12
4D-ben: 0+2+4+6+8=20
5D-ben: 0+2+4+6+8+10=30
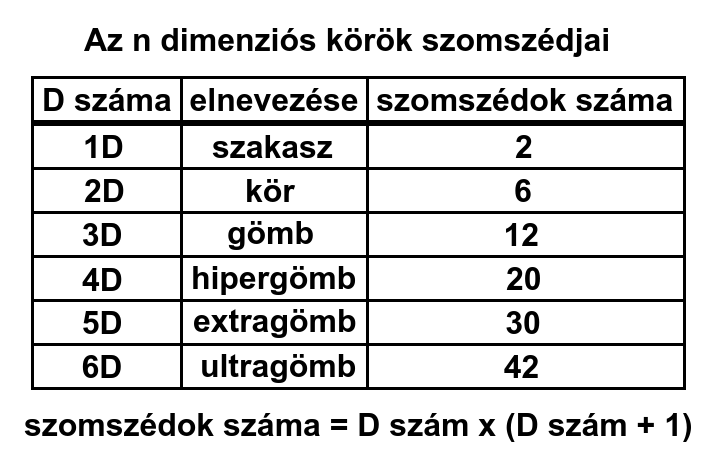
6D-ben: 0+2+4+6+8+10+12=42
Ez megfelel a páros számok összegének, ami: nx(n+1).


2. MISZTIKA
Az időfizika és számmisztika kedvelőinek figyelmébe ajánlom a következő összefüggéseket:
1. Az alfatéri szerinó által keltett természetes téridő térdimenziószáma maximum 6D lehet, mivel az időhurok 5 tachionja legfeljebb 5 különböző irányba tud mozogni egymáshoz képest az őskáoszban és ezt az 5D-s hurkot harmadlagos csavarodással 6D-ssé lehet felbővíteni, tovább nem. A 6D-ben 42 szomszédja lehet maximum egy gömbnek (időhuroknak), ami közismerten a végső válasz az univerzummal, az élettel és mindennel kapcsolatos kérdésekre (az élet száma).
2. A szomszédok száma 7D-ben: 56, 8D-ben: 72. A fotinók által keltett természetes fényidő fénydimenziószáma maximum 8D lehet, mivel az időhurok 7 tachionja legfeljebb 7 különböző irányba tud mozogni egymáshoz képest egy mesterségesen felbővített alfa vagy bétatérben. Ezt a 7D-s hurkot harmadlagos csavarodással 8D-ssé lehet felbővíteni, tovább nem. A 8D-ben 72 szomszédja lehet maximum egy gömbnek, ami a kerubok (isten körül álló angyalok) száma az isteni hierarchiában.
3. Hogy mennyire fontos kutatási téma az n dimenziós gömbök pakolási problémája, azt jól mutatja, hogy 2022-ben Marjna Viazovszka ukrán matematikusnő Fields-érmet nyert a gömbök nyolcdimenziós elrendezéséért. Lásd:
https://index.hu/tudomany/2022/07/20/fields-dij-matematika-gomb-elrendezes-kvantum-viazovszka-ukrajna/
Első kérdés: Hány további, külső szomszédja van az n dimenziós kör szomszédainak?
1D-ben: 2.
2D-ben: 12.
3D-ben: 44.
4D-ben: ?.
A körök száma összesen:
1D-ben: 3+2=5.
2D-ben: 7+12=19.
3D-ben: 13+44=57.
4D-ben: ?.
Második kérdés: Hány további, külső szomszédja van az n dimenziós kör szomszédai szomszédainak?
1D-ben: 2.
2D-ben: 18.
3D-ben: 96.
4D-ben: ?.
A körök száma összesen:
1D-ben: 5+2=7.
2D-ben: 19+18=37.
3D-ben: 57+96=153.
4D-ben: ?.
Harmadik kérdés: Hány további, külső szomszédja van az n dimenziós kör szomszédai szomszédai szomszédainak?
1D-ben: 2.
2D-ben: 24.
3D-ben: 170.
4D-ben: ?.
A körök száma összesen:
1D-ben: 7+2=9.
2D-ben: 37+24=61.
3D-ben: 153+170=323.
4D-ben: ?.

Ebből látható, hogy 1D-ben mindig +2-vel nő a számuk. 2D-ben lépésenként +6-tal lineárisan nő a számuk. 3D-ben pedig párhuzamos síkrétegekre bontással lehet meghatározni a számukat. Mivel a 3D-s gömb szomszédok modellje olyan, mint a több, egymásra rétegezett 2D-s kör szomszédok modellje. A középső síkban egy kör körül 6-tól indulva, +6-tal nő rétegenként a körök száma (6, 12, 18, 24, 30, stb.), így a számuk összesen: 7, 19, 37, 61, 91, stb. A vele szomszédos, alatta és fölötte lévő síkokban három kör körül 9-től indulva, +6-tal nő héjanként a körök száma (9, 15, 21, 27, 33, stb.), így a számuk összesen: 12, 27, 48, 75, 108, stb. A további, ezek alatt és fölött lévő síkokban az egy körös és három körös középpontú síkok váltogatják egymást, eggyel csökkenő rétegszámokkal. Ezen a módon, "brute force" módszerrel n rétegig kiszámolható a szomszédok összesített száma, amennyiben nem akar az ember egy csomó ping-pong labdát összeragasztani. Az alábbi képletsort így tudtam elkészíteni.
Első szomszédok három rétegben: 3+7+3=13
Második szomszédok öt rétegben: 7+12+19+12+7=57
Harmadik szomszédok hét rétegben: 12+19+27+37+27+19+12=153
Negyedik szomszédok kilenc rétegben: 19+27+37+48+61+48+37+27+19=323


Elvileg ezen a módon úgy lehet a magasabb térdimenziókra vonatkozó eredményeket előállítani, ha a 4D-s hipergömb szomszédok modelljét több, egymásra rétegezett 3D-s gömb szomszédok modelljére bontjuk. Ezt a feladatot (és az 5D-s, 6D-s kiterjesztéseket) azonban már nem végeztem el, hogy az Olvasóknak is hagyjak némi munkát. Akinek sikerül kiszámítani az eredményeket, írja meg, mire jutott, hogy hozzátehessem ehhez a cikkhez!


A szomszédossági probléma jelentősége az n dimenziós atomfizikában van, ahol a részecskék időtartályait megtöltő fotinók számának növekedése adott számú lépés után meghaladja a körülöttük rendelkezésre álló helyet, leállítva az időfraktálok növekedését. Ez korlátozza le minden térdimenziószinten a részecskék fizikai méretét, fotinószámát és tömegét. Részletesen lásd: A neutron belső szerkezete (2021, létfilozófia) és: Az elektron belső szerkezete (2023, létfilozófia) című írásokban.

4. MÁSFAJTA TÉRKITÖLTÉSEK
Az Alan L. Mackay-ikozaéder egy gömbökből felépülő ikozaéder alakú klaszter, ami szerkezetileg némiképp eltér a gömb pakolási problémától, így lépésenként egyre kevesebb gömböt tartalmaz, a nem tökéletes térkitöltése miatt.
Ennek képlete: C=(10xn^3-15xn^2+11xn-3)/3 ahol n az egy élen lévő gömbök száma. A gömbök száma a klaszterben rétegenként így növekszik: 1, 13, 55, 147, 309, 561, 923, 1415.
Lásd: Ikozaéder – Wikipédia ( https://hu.wikipedia.org/wiki/Ikoza%C3%A9der )
Az Almássy Zoltán-féle ikozaéder egy aranymetszéssel torzított ikozaéderekből felépülő, ikozaéder alakú klaszter, ami szerkezetileg üreges. Egyrészt torzított ikozaéderekből épített üreges testek sorozata, amik egymásba építhetők. Másrészt, mindegyik test tetraéder alakú üregeket tartalmaz. Ez a szerkezet dodekaéderekkel is megépíthető.
Ebben az n-edik ikozaéder réteg torzított ikozaédereinek száma: 12, 92, 252... A kiszámítási képlete: Sˇn=40xn^2-40xn+12 ahol n>0 természetes szám.
Lásd: Almássy-féle ikozaéder – Wikipédia ( https://hu.wikipedia.org/wiki/Alm%C3%A1ssy-f%C3%A9le_ikoza%C3%A9der )
Készült: 2023.05.19. - 06.12.
Frissítve: 2023.07.31., 2023.12.28.
Következő írás
Vissza a tartalomhoz