10. KÖZISMERT SZALAGÁBRÁK
Amint az észrevehető volt az eddigi képsorozatokon, egyes szalagok ismerős geometriai mintákba lettek elrendezve. Nem véletlenül. A világ vallásai, a népművészetek és az építészet tele vannak olyan ősi, egyetemesen használt szimbólumokkal, amik a teremtés fontosabb lépéseit rejtik magukban. Az alábbiakban ezeket soroljuk fel külön, a rajzolt változattal kiegészítve, pár szavas magyarázattal. A szimbólumok pontosabb (és valószínű) jelentését a következő fejezetben boncolgatjuk.
A síkba kilapított Möbius-szalag háromszöge.:

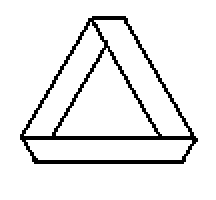
A síkba kilapított két Tetrás-szalag, mint nyolcágú csillag, két négyzetből összerakva.:

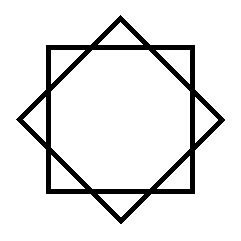
Az aszimmetrikusan felhasított Möbius-szalag és két Tetrás-szalag.:

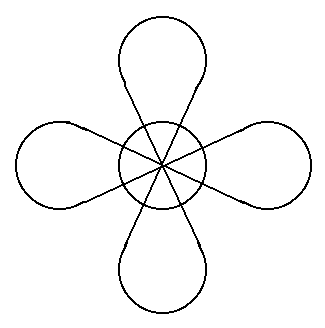
A két Tetrás-szalag önmagában.:

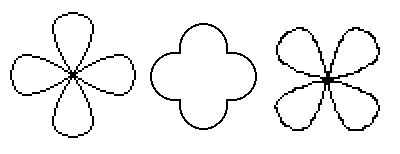
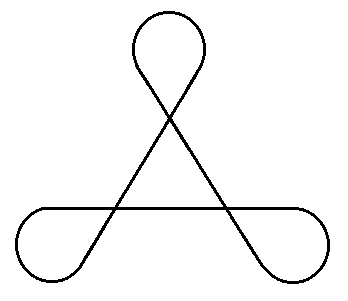
A Háromhurkos-szalag (lekerekített rajz). A
csúcsos változatot egy keresztben összeragasztott Szimplás és
Tetrás-szalag szimmetrikus felhasításakor kapjuk. A hatszirmú
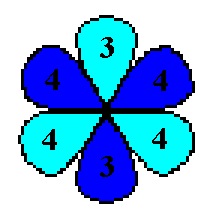
virág két Háromhurkos-szalag (eltérő színnel jelölve). A
hurkokba írt számok azt jelzik, hogy az adott hurkon hány szalag
halad keresztül a gubancban.
Megjegyzés 1.: Az Artúr-mondakört feldolgozó
Excalibur című filmben a Kerek Asztal lovagjai egy olyan asztal
körül gyűltek össze a palotában, amire két Háromhurkos-szalagot
festettek, eltérő színnel.
Megjegyzés 2.: Számos szalagot hajlékony
újságpapírból is megcsináltunk, amivel könnyebb bánni, mint a
kartonpapírral, s addig kisérleteztünk velük, míg az alább több
helyen felbukkanó ábrákat kaptuk.

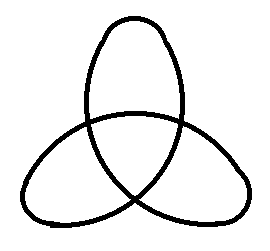
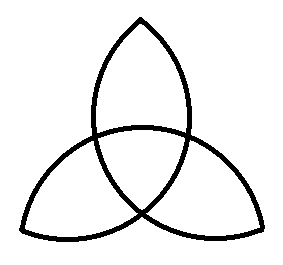
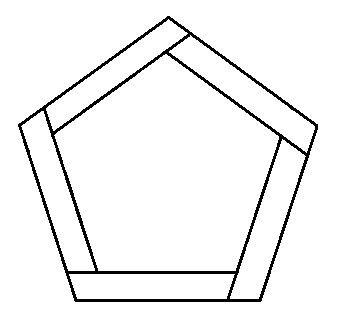
Egy Pentás-szalag síkba kilapítva.:

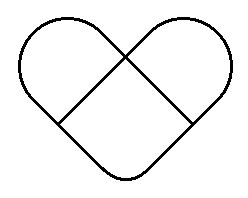
Egy Öthurkos-szalag kifeszíthető pentagrammának vagy kettős(-nek látszó) szívnek is. Az utolsó (ej5s1er) rajz egy bármely pékségben kapható sósperec akarna lenni, összehasonlításképpen. Figyelemreméltó, hogy milyen sok ételünk formája hordoz magán időfizikai információkat. Erről később külön értekezést fogunk közzé tenni...


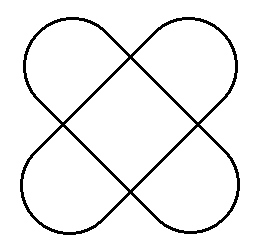
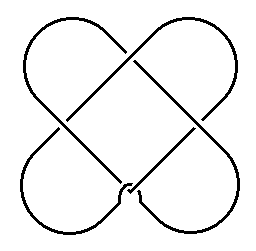
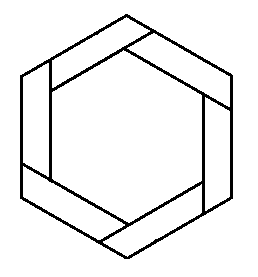
Egy Hexás-szalag síkba kilapítva és térben.:


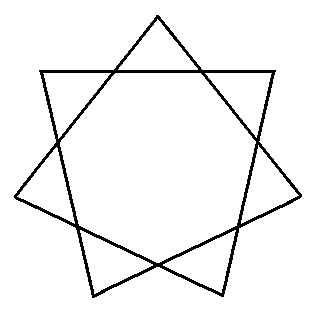
Egy Héthurkos-szalag, ami hétágú csillagot formáz, de kifeszíthető másképp is (torz pentagrammát is lehet belőle csinálni némi ügyeskedéssel). Ahol a fekete pont van, ott bonyolult csomó burjánzik.:
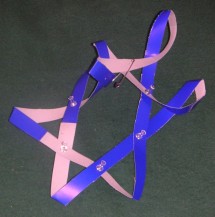
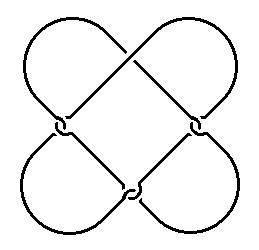
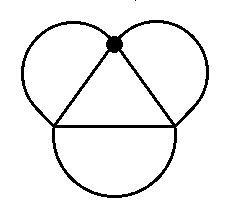
Egy Kilenchurkos-szalag.:

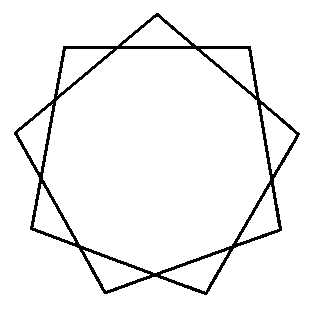
Két Nullás-szalag kétszeresen hosszában összeragasztva. Sok növény termése néz ki így.:

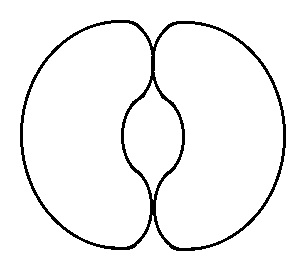
Hosszában összeragasztott szalagok felhasításai.:

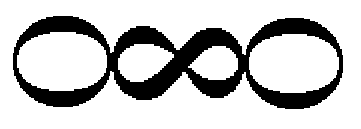

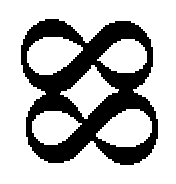
Keresztben összeragasztott szalagok felhasításai.:

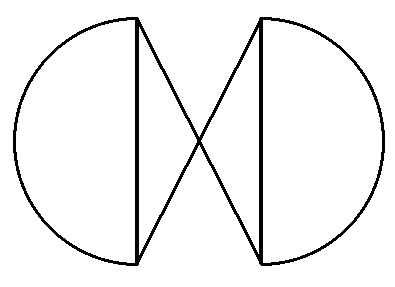
A szív alakzat, ami számos helyen felbukkan a teremtésben.:


Egy balos Duplás és egy jobbos Szimplás-szalag keresztben összeragasztva és felhasítva nagyon ismerős formákat tud produkálni.:

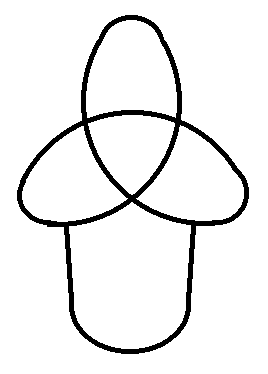



További érdekes geometriai szerkezetek.:





Az alábbi három formációra ugyancsak az újságpapíros szalagok húzgálása közben bukkantunk. Az első (k2j3j3s2br) rajz két keresztben összeragasztott Triplás-szalag felhasításából készül. A második (k2j3j4s2br) egy Triplás és egy Tetrás-szalag ugyanezen a módon megcsinálva, a harmadik pedig (k2j4j4s2br) két Tetrás-szalagból lesz.
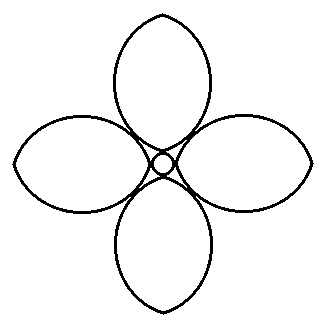
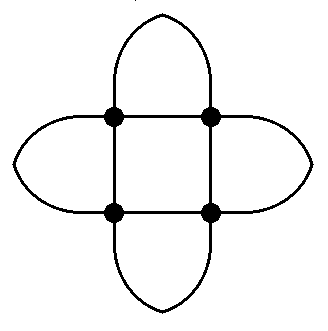
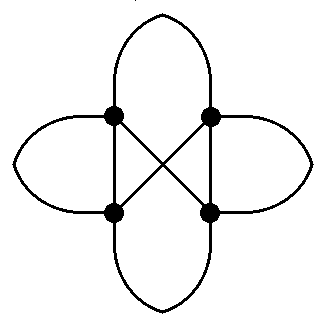
Ahol a geometriai szerkezet figyelemreméltó szabályosságokat produkál, ott érdemes tovább kutatni, hisz tudjuk, hogy a természetnek van szépérzéke...