| 1. | Adott két halmaz: |
| A = {egyjegyű pozitív páratlan számok} | |
| B = {2; 3; 5; 7} | |
|
Sorolja fel az A |
I. rész
A feladatok megoldására 45 perc fordítható, az idő leteltével a munkát be kell fejeznie.
A feladatok megoldási sorrendje tetszőleges.
A feladatok megoldásához zsebszámológépet és négyjegyű függvénytáblázatot használhat, más elektronikus vagy írásos segédeszköz használata tilos!
A feladatok végeredményét az erre a célra szolgáló keretbe írja, a feladatok megoldását csak akkor részletezze, ha erre a feladat szövege utasítást ad!
A feladatok megoldását tollal készítse! Ha valamilyen megoldást vagy megoldásrészletet áthúz, akkor az nem értékelhető!
Az egyes feladatokra az ott feltüntetett pontszámnál több nem kapható.
Ha a megadott válasz hibás elemet vagy elemeket tartalmaz, akkor maximális pontszám nem adható.
| 1. | Adott két halmaz: |
| A = {egyjegyű pozitív páratlan számok} | |
| B = {2; 3; 5; 7} | |
|
Sorolja fel az A |
|
Az A |
1 pont |
|
|
Az A \ B halmaz elemei: |
1 pont |
|
|
2. |
Jelölje be, hogy az alábbi egyenlőségek igaz vagy hamis állítások! ( |
|
) |
a) a3 ∙ a4
= a12
|
Az állítás igaz vagy hamis. |
1 pont |
|
b) a8 : a2 = a4
|
Az állítás igaz vagy hamis. |
1 pont |
|
| 3. | Adott a következő hétjegyű szám: 135947X. Milyen számjegyeket írhatunk az X helyére, hogy az így kapott hétjegyű szám 4-gyel osztható legyen? |
|
Az X értéke: |
2 pont |
|
| 4. | Oldja meg a következő egyenletet a valós számok halmazán! |
|
3x = 81 |
|
Az egyenlet megoldása: |
2 pont |
|
| 5. | Hozza egyszerűbb alakra a következő kifejezést! Írja le a megoldás egyes lépéseit! | |
|
|
, x Î R \ {1} | |
|
|
1 pont |
|
|
A kapott kifejezés: |
1 pont |
|
| 6. | Hányféleképpen lehet egy 10 fős társaságból egy elnököt és egy titkárt választani? Megoldását indokolja! |
|
|
1 pont |
|
|
A lehetőségek száma: |
1 pont |
|
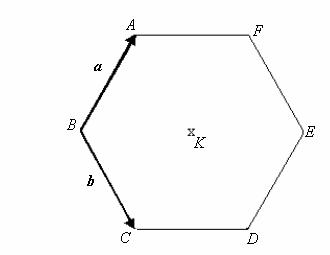
| 7. | Egy szabályos hatszög csúcsai: A, B, C, D, E, F, középpontja K. |
|
Legyen
|
|
|
Fejezze ki a megadott vektorok
segítségével a |
|
|
1 pont |
|
|
|
2 pont |
|
| 8. | Egy szabályos pénzérmét háromszor feldobunk. Mekkora az esélye, hogy egyszer fejet és kétszer írást kapjunk? Megoldását indokolja! |
|
|
2 pont |
|
|
Az esély: |
1 pont |
|
| 9. | Oldja meg a következő egyenletet a valós számok halmazán! Megoldását indokolja! |
|
|
|
|
2 pont |
|
|
A megoldás: |
2 pont |
|
|
10. |
Milyen valós x-ekre értelmezhetők a következő kifejezések? |
|
|
|
a) |
|
|
Az értelmezési tartomány: |
2 pont |
|
|
|
b) |
|
|
Az értelmezési tartomány: |
2 pont |
|
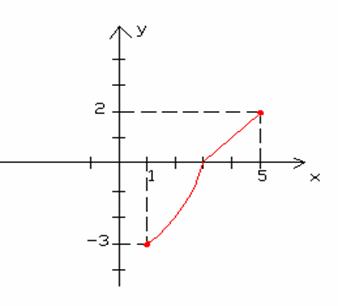
| 11. | Mi az alábbi, grafikonjával megadott függvény értelmezési tartománya és értékkészlete? |
|
Értelmezési tartomány: |
2 pont |
|
|
Értékkészlet: |
2 pont |
|
II. rész
A feladatok megoldására 135 perc fordítható, az idő leteltével a munkát be kell fejeznie.
A feladatok megoldási sorrendje tetszőleges.
A II/B részben három feladat közül csak kettőt kell megoldania. A nem választott feladat sorszámát írja be a dolgozat befejezésekor az alábbi négyzetbe! Ha a javító tanár számára nem derül ki egyértelműen, hogy melyik feladat értékelését nem kéri, akkor az utolsó feladatra nem kap pontot!
|
|
A feladatok megoldásához zsebszámológépet és négyjegyű függvénytáblázatot használhat, más elektronikus vagy írásos segédeszköz használata tilos!
A feladatok megoldásához alkalmazott gondolatmenetét minden esetben írja le, mert a feladatra adható pontszám jelentős része erre jár!
Ügyeljen arra, hogy a lényegesebb részszámítások is nyomon követhetőek legyenek!
A feladatok megoldásánál használt tételek közül az iskolában tanult, névvel ellátott tételeket (pl. Pitagorasz-tétel, magasság-tétel) nem kell pontosan megfogalmazva kimondania; elég csak a tétel megnevezését említeni, de alkalmazhatóságát röviden indokolni kell.
A feladatok végeredményét (a feltett kérdésre adandó választ) szöveges megfogalmazásban is közölje!
A feladatok megoldását tollal készítse! Ha valamilyen megoldást vagy megoldásrészletet áthúz, akkor az nem értékelhető.
Az egyes feladatokra az ott feltüntetett pontszámnál több nem kapható.
Ha a megadott válasz hibás elemet vagy elemeket tartalmaz, akkor maximális pontszám nem adható.
II/A
| 12. | Kör alakú amfiteátrum küzdőterének két átellenes pontjában áll egy-egy gladiátor, az uralkodó a pálya szélén ül. A gladiátorok egyenes vonalban odafutnak az uralkodóhoz. Az egyik 20 métert, a másik eggyel többet tesz meg, amíg odaér. Mekkora az amfiteátrum sugara? Készítsen ábrát is a megoldáshoz! |
|
|
|
12 pont |
|
Megoldás:
| 13. | Magyarországon egy átlagos család egy főre eső napi vízfogyasztása 152 liter. Ez a fogyasztás több részből tevődik össze: főzés, mosogatás, WC-használat, mosakodás, mosás, egyebek. A felsoroltak vízfogyasztási aránya rendre 4%, 4%, 25%, 26%, 30%, 11%. A vízdíj 140 Ft/m3. |
a) Ha minden egyes mosásnál egy takarékosabb mosógéppel 25%-kal kevesebbet használunk, akkor – a lakosság létszámát 10 millióra kerekítve – hány m3 vizet takarít meg az ország lakossága egy év (365 nap) alatt?
|
|
|
6 pont |
|
b) Ez hány százaléka az összes vízfogyasztásnak?
|
|
|
3 pont |
|
c) Mennyi naponta a lakossági megtakarítás értéke összesen? Az eredményt adja meg normálalakban is!
|
|
|
3 pont |
|
Megoldás:
| 14. | Egy adatsor öt számból áll, amelyből kettő elveszett, a maradék három: 3; 4; 7. Tudjuk, hogy a módusz 4, és az adatok átlaga (számtani közepe) 6,5. |
a) Mi a számsor hiányzó két adata? Válaszát indokolja!
|
|
|
5 pont |
|
b) Mennyi az adatok mediánja? Válaszát indokolja!
|
|
|
3 pont |
|
c) Számolja ki az adatok szórását!
|
|
|
4 pont |
|
Megoldás:
II/B
|
A 15. – 17. feladatok közül tetszés szerint választott kettőt kell megoldania. |
| 15. | Reklámcélokra tömör fémből készült dísztárgyakat gyártanak. Ha olyan négyzet alapú szabályos gúla alakúakat öntenek, ahol a gúla alapéle is, magassága is 5 cm, akkor 100 darabra elég a nyersanyag. |
a) Mekkora a nyersanyag térfogata?
|
|
|
3 pont |
|
b) Mennyibe kerülne a 100 gúla befestése, ha 1 m2 felület festési költsége 1200 Ft?
|
|
|
7 pont |
|
Az ellenőrzés során kiderült, hogy az elkészült dísztárgyak 5%-a selejtes. A 100 gúlát tartalmazó dobozból véletlenszerűen nyolcat választunk ki.
c) Hányféleképpen lehet ezt megtenni?
|
|
|
2 pont |
|
d) Mennyi az esélye, hogy a nyolc darab kiválasztott gúla közül éppen 3 darab lesz selejtes?
|
|
|
5 pont |
|
Megoldás:
|
16. |
a) Mutassa meg, hogy a |
|
egyenletnek a valós számok körében |
|
csak a 4 és a 9 a megoldásai! |
|||
|
|
|
5 pont |
|
|
|
b) Egy számtani sorozat első tagja a |
|
egyenlet nagyobbik gyöke, |
|
|
a számtani sorozat különbsége pedig az egyenlet kisebbik gyöke. |
||
|
Adja meg e számtani sorozat első 5 tagjának az összegét! |
|||
|
|
|
4 pont |
|
|
|
c) Ha e sorozat első n tagjának összege 3649, akkor mennyi az n értéke? |
|
|
|
8 pont |
|
Megoldás:
|
17. |
Írja fel annak a két egyenesnek az egyenletét, amelyek párhuzamosak a 3x – 4y = 0 |
|
|
egyenletű egyenessel, és érintik az x2 + y2 – 2x + 4y – 20 = 0 egyenletű kört! |
|
|
|
17 pont |
|
Megoldás: