A modellrepülés elmélete (7)

<< előző rész  |  következő rész >>

Példa: (folytatása)

A kiszámított C_f » 0,64 felhajtóerő-tényezőhöz tartozó C_e ellenállás tényezőt a szárnyszelvény mérési görbéjéből kell kikeresni. Olyan görbét kell találni, amelyik Re = 100 000 vagy hozzá közeli értékre vonatkozik.

Schmitz mérései között találunk Re = 105 000 - nél mért adatokat az N 60 jelű szelvénynél. Itt 1 : Y oldalviszonynál a C_f = 0,65 - höz C_e = 0,0227 tartozik. Számítsuk ki még hozzá az indukált ellenállás tényezőjét:

az összes ellenállás tehát:

C _ei(11) = 0,0227+0,0349 = 0,0349

A szárny siklása így:

0,0349:0,65 = 1:18,6

és a merülősebessége:

w = 6,5:18,6 = 0,35 m/s

(és akkor nem vettük figyelembe a törzs és a csillapító ellenállását.)

Ez a számítás ellipszis alapú szárnyra vonatkozott. Számítsuk ki ugyanezt a szárnyat téglalap alaprajz esetén. Glauert szerint téglalap szárny esetén az indukált ellenállás-tényező a következő képlettel számítható - közelítőleg:

ahol d = az oldalviszonytól függő érték. A nem végtelen oldalviszony (l = 11) miatt az indukált ellenállás képlete is változik:

A l és a t értékei - az oldalviszonytól függő értékek:

l	1:3	1:4	1:5	1:6	1:7	1:8	1:9	1:10	1:11
d	0,016	0,026	0,037	0,046	0,055	0,064	0,072	0,080	0,088
t	0,097	0,122	0,145	0,163	0,183	0,201	0,216	0,288	0,240

Ezek az értékek abban az esetben pontosak, ha a C_f / a Y értéke a felhajtóerő-tényező görbéjének egyenes szakaszán az elméleti 2p = 6,28 érték. Más esetben az értékek csak közelítő jellegűek, jelen esetben azonban teljesen megfelelők.

Téglalap szárny esetén az indukált ellenállás tényezője tehát így adódik:

Az ellenállás-tényező tehát

így a szárny siklószáma:

és merülősebessége:

Így az elméleti számítás szerint az egyedülálló szárny siklása

1:18,6 - ról 1:18 - ra,

merülősebessége pedig

0,35 m/s - ról 0,36 m/s - ra

romlik, ha ellipszis helyett tiszta téglalap formát alkalmazunk (ugyanolyan oldalviszony mellett!)

A törzs és a csillapítók ellenállása - és az összes ellenállás

Vegyük most tekintetbe a törzs és a csillapítók ellenállását is. Induljunk ki a gyakorlati mérés eredményéből, feltételezzük hogy a sikló-mérésnél a modell siklószáma 1:13 - nak bizonyult, téglalap szárnnyal.

A siklószám az összes ellenállás és a felhajtóerő-tényező hányadosa, tehát így:

, amiből

Mint már kiszámítottuk, a téglalap szárny teljes ellenállás-tényezője:

így a törzs (C_et) és a csillapítófelületek C_ecs) együttes ellenállását - mely állandó érték - megkapjuk, ha az összes ellenállás-tényezőből a szárnyét levonjuk.

Ez a törzs és a csillapítók ellenállás-tényezője a szárnyfelületre vonatkoztatva.
Elliptikus szárny esetén a gép teljes ellenállás-tényezőjét (C_eö) úgy kapjuk meg, hogy a szárny ellenállás-tényezőjéhez hozzáadjuk a törzs és a csillapítók együttes tényezőjét. Így:

Ellipszis szárnyú modell siklószáma a téglalap formára kimért 1:13 értékével szemben:

- ra javul,

merülése pedig

m/s - ról

m/s - ra csökken

A teljesítmény szempontjából döntő merülő-sebességnél tehát a téglalap szárny mindössze 1 cm/s értékkel rosszabb, mint az ellipszis. Ez az érték oly csekély, hogy a modell-méréseknél gyakorlatilag ki sem mutatható, mert kisebb, mint a mérési pontosság.

A trapéz szárny a kettő közé esik, így levonhatjuk azt a következtetést, hogy a merülősebesség és a siklószám szempontjából a repülőmodelleknél a téglalap, trapéz és elliptikus szárnyak között nincs gyakorlati különbség.

Ez a magyarázata annak hogy a gyakorlatban már nincsenek is szépen lekerekített - szinte ellipszis-végű - szárnyak. Ezek lehetnek nagyon szépek, de csak egy árnyalattal jobbak a téglalap, vagy a trapéz szárnyaknál, szerencsétlen esetben pedig rosszabbak.

A nagyon “kihegyezett” , nagyon elkeskenyített szárny vége - a szelvény hosszának csökkenése miatt - kisebb Reynolds - számmal repül, mint a középrész. Ha ezt a modellt szűk körre állítjuk be, nagyon könnyen előfordulhat hogy a kicsi körözési sugár miatt a belső szárnyvég “átesik”, a modell egyre szűkülő körrel jön a föld felé: “bedugózik”

A körözési sugár és a Reynolds - szám

A repülőmodellek szabadon repülésüket körözésre beállítva végzik. Az egyes modellekre jellemző a repülés közben tett körök átmérője (D) vagy ennek fele: a sugara (r)

A szűk körözésre beállított modellek hajlamosak ennek a körnek sugarát “beszűkíteni”, illetve “dugóhúzóba esni”.

Ennek a beszűkülésre hajlamosságnak oka elsősorban a kicsi körözési sugár, magyarázata - oka - a körözés közben a két szárnyvég sebesség-különbsége, aminek következménye az, hogy a szárny két vége nem azonos Reynolds -számmal repül.

Repülési sebességnek vesszük a törzs középvonalának sebességét, akkor körözés közben a “belső” szárny lassabban, a “külső” gyorsabban repül, mint a középvonal.

Példa:

A modell fesztávolsága: 2 méter, szárnymélység 15 cm.
A szárny alaprajza téglalap
A körözés sugara: r = 10 méter,
Repülési sebesség v = 5 m/s

A modell középvonala - törzse - ezzel a sebességgel egy kör alatt teszi meg a kör kerületét, (K) azaz

utat tesz meg, tehát egy kör repülési ideje (t)

Ezzel a sebességgel körözve a szárny “belső” vége kisebb sugáron mozog, ezért rövidebb utat tesz meg ugyanannyi idő alatt. A belső szárnyvég körözési sugara: r =10 -1= 9 méter, tehát a megtett út ennek a körnek a kerülete: (K _belső)

az idő ugyanannyi, tehát a “belső” szárnyvég sebessége:

A külső szárnyvégen: (K_külső)

A sebesség különbség ilyen egyszerű esetben is jelentős. Számítsuk ki, ez a sebesség-különbség mekkora Reynolds-szám különbséget jelent: A belső szárnyvégen:

és a külső szárnyvégen :

Nagyobb fesztávú modelleknél ez a különbség még jelentősebb. Ha a szűk kör miatt a belső szárnyvég a kritikus R_e szám alá kerül, az áramlás leválik, az ellenállás megnő és a modell egyre szűkebb köröket leírva ütközik a földnek. Ez a “bedugózás” leggyakrabb oka.

A szárny alaprajza és a Reynolds - szám

A szabadonrepülő modellek oldalviszonya - a korszerű, nagy szilárdságú anyagok következtében - a nagyon nagy fesztávolságú modellek irányába tolódott el. Ma már az 1:10 - 1:12 oldalviszony csak kezdő, vagy gyakorló modelleknél fordul elő.

Nagy teljesítményű versenymodell (F1A) adatai (a példához)

fesztávolsága 2400 mm,
szárnymélység középen 140 mm,
szárnymélység a szárny végén 90 mm.
szárnyfelület 30 dm²
oldalviszonya: (l )

l =

Ha a modell sebessége 5 m/s, a szárnyközép R_e száma:

a szárny-fül végének Re száma:

Ennek a modellnek köröztetésével már nagyon óvatosan kell bánni, mert a keskeny fül végének Re száma olyan alacsony hogy nagyon könnyen a kritikus alá kerülhet, ami a már ismert dugóhúzóhoz vezet.

Egyik megoldás a sebesség növelése, de ez csak az állásszög csökkentésével érhető el (ha nem akarjuk a súlyát növelni) ekkor a beállított legkisebb merülősebességet adjuk fel (amit nem érdemes.)

Ezért a nagy fesztávú modelleket általában nagy sugarú kör repülésére állítják be, hogy a szárny két végének Re száma között kicsi legyen a különbség.

Az alaki ellenállás és a felületek csatlakozása

(Ezekre elsősorban nagyobb méretű versenymodellek tervezésénél érdemes figyelni.)

1. A törzs és a szárny csatlakozása

Ha két áramlásban lévő test egymáshoz közel helyezkedik el, a körülöttük kialakuló áramlás kölcsönösen megzavarja határrétegeiket, ezért a súrlódási ellenállás ilyen helyeken megnő. Nem kedvező az egymásra-hatás akkor, ha a két egymás közelében lévő test körül az áramlás először gyorsul, azután a széttartó felületek között ismét lelassul. Ilyenkor az áramlás könnyen leválik, ezt a jelenséget diffuzor - hatásnak nevezik. Ez a hatás összefügg a szárny és a törzs egymáshoz viszonyított elhelyezkedésével.

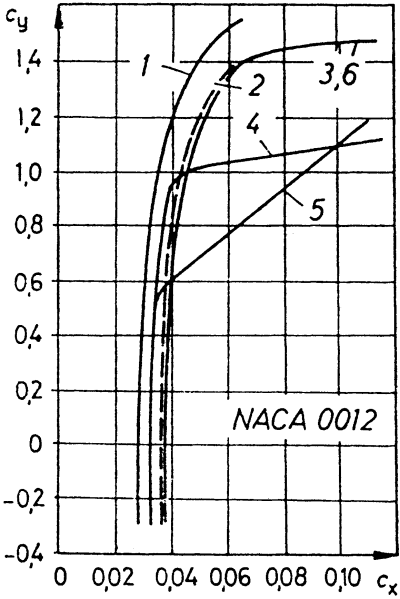
Az ábrán egy szárny polárgörbéjét ábrázolták különféle szárny-törzs elrendezések esetén.

<< előző rész  |  következő rész >>