|
A modellrepülés elmélete (8)
<<
előző rész | következő rész >>
(Az előző résznek
ebből a fejezetéből néhány sor kimaradt, ezért megismételjük elölről -
kijavítva.
A szárny alaprajza - oldalviszonya - és
a Reynolds - szám
A szabadonrepülő
modellek oldalviszonya - a korszerű, nagy szilárdságú anyagok következtében
- a nagyon nagy fesztávolságú modellek irányába tolódott el. Ma már az 1:10
- 1:12 oldalviszony csak kezdő, vagy gyakorló modelleknél fordul elő.
A sokkal nagyobb
oldalviszony mellett a szárnyvégek is keskenyebbek, mint a középrész. E
“trapéz” szárny-megoldásnak szilárdságtani okai is vannak - a szándékos
oldalviszony-javítás mellett.
Az előző példában egy
“gyakorló” méretű modell Re számát számítottuk ki, már ennél is számottevő
volt a két szárnyvég közötti Re-szám különbsége. Egy korszerű. nagy
fesztávú modell esetén ez a különbség sokkal nagyobb!
Nagy teljesítményű
versenymodell (F1A) adatai (a példához)
fesztávolsága 2400 mm,
szárnymélység középen 140 mm,
szárnymélység a szárny végén 90 mm.
szárnyfelület 30 dm2
oldalviszonya: (l )
l = 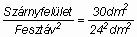 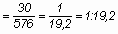
Ha a modell sebessége 5
m/s, a szárnyközép Re száma:
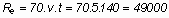
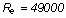
Ezzel a szárnyközép (a
törzs középvonala) által megtett út (a kör kerülete):
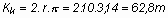
sebessége 5 m/s, tehát
egy kör repülési ideje:(t)
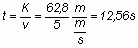
A szárny belső füle
kisebb sebességgel repül, ezért - ha a körözési sugarat ismét r = 10 m. -
nek számítjuk, a belső szárny-fül végének repülési sugara:
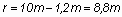
a kör kerülete:
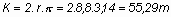
Egy kör repülési ideje
(t) ugyanannyi, mint a középvonal körözési ideje, ezért a kisebb sugáron
repülő belső szárnyvég sebessége:
 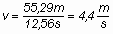
Re száma:
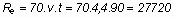
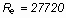 ! !
Ez a Re szám alig
nagyobb mint a fele a szárnyközép Re számának!
Ennek a modellnek
köröztetésével már nagyon óvatosan kell bánni, mert a keskeny fül végének
Re száma olyan alacsony hogy nagyon könnyen a kritikus alá kerülhet, ami a
már ismert dugóhúzóhoz vezet.
Egyik megoldás a
sebesség növelése, de ez csak az állásszög csökkentésével érhető el (ha nem
akarjuk a súlyát növelni,) ekkor a beállított legkisebb merülősebességet
adjuk fel, (amit nem érdemes.)
Ezért a nagy fesztávú
modelleket általában nagy sugarú kör repülésére állítják be, hogy a szárny
két végének Re száma között kicsi legyen a különbség.
Az alaki ellenállás és a felületek
csatlakozása
(Ezekre elsősorban
nagyobb méretű versenymodellek tervezésénél érdemes figyelni.)
1. A törzs és a szárny csatlakozása
Ha két áramlásban lévő
test egymáshoz közel helyezkedik el, a körülöttük kialakuló áramlás
kölcsönösen megzavarja határrétegeiket, ezért a súrlódási ellenállás ilyen
helyeken megnő. Nem kedvező az egymásra-hatás akkor, ha a két egymás közelében
lévő test körül az áramlás először gyorsul, azután a széttartó felületek
között ismét lelassul. Ilyenkor az áramlás könnyen leválik, ezt a
jelenséget diffuzor - hatásnak nevezik. Ez a hatás összefügg a szárny és a
törzs egymáshoz viszonyított elhelyezkedésével.
Az ábrán egy szárny
polárgörbéjét ábrázolták különféle szárny-törzs elrendezések esetén.

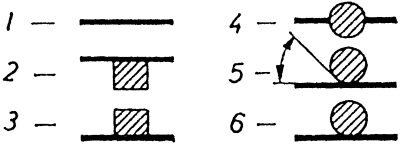
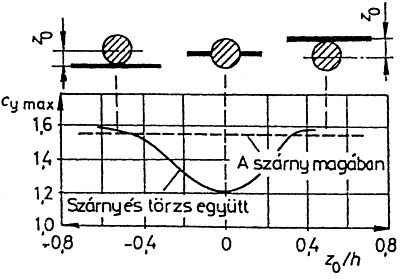
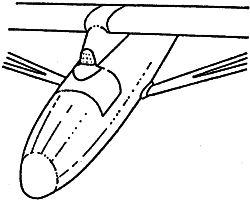
Magas-szárnyú gépeknél
akkor csökkenthető a legkisebbre, a diffuzor - hatás, ha a szárny és a
törzs közötti szög nagy.
Középszárnyú gépek
esetén a legkedvezőtlenebb az ellenállás, de a gépek egyéb hibáihoz
viszonyítva nem érdemes nagyon bonyolult, hosszú átmenetet igénylő
megoldásokat tervezni - akkor sem, ha aerodinamikailag az a kedvező:

Sokkal előnyösebb egy
egyszerű de áramlástanilag jól megoldott kialakítást választani.
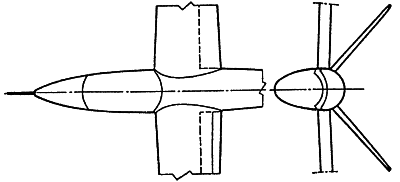
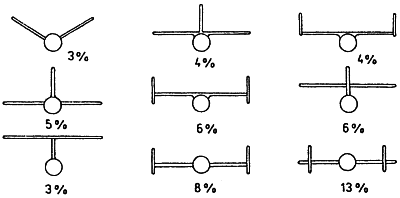
2. A törzs és a vezérsíkok csatlakozása
és kialakítása is befolyásolja
az alaki ellenállást. Az összes ellenállásnak százalékában mutatja az
előforduló megoldásokat a következő ábrán:
Kísérleti siklómérések
Felmerült a
szükségessége annak hogy a repülőmodellek számított teljesítményeit a
gyakorlatban is ellenőrizzük. A modellt ilyenkor teljesen egyenes
repülésre, nyugodt siklásra kell beállítani A szabadban való mérés eredményei
általában sok hibaforrást rejtenek magukban, mert a legkisebb vízszintes -
vagy függőleges - légáramlás jelentősen befolyásolja a mérések eredményeit
Mérések céljára a
nagyméretű termek, csarnokok, hangárok felelnének meg a legjobban, de
nekünk nem sok ilyen hely áll rendelkezésünkre. Meg kell elégednünk olyan
időjárás kiválasztásával, amikor a levegő mozgása - szinte teljesen -
megszűnik, termikképződés sincs és elég nagy, vízszintes, akadálymentes
terület áll rendelkezésünkre.
Még ebben az esetben is.
ajánlott a méréseket a repítésre alkalmas területen oda-vissza, azaz
mindkét irányból elvégezni, hogy a mérések átlagolásánál a szélcsendben is
meglévő kicsi, szinte nem is érezhető légmozgás okozta eltéréseket is ki
tudjuk küszöbölni.
A siklatásokat mindig
azonos magasságból kell elvégezni. Ennek érdekében ajánlott egy állványt
készíteni, amelyről a modell indítható. Az állvány a várható siklás
szögének megfelelően lejtős legyen az indítás iránya felé.
A siklatáshoz a modellt
mindig azonos erővel kell indítani. Ez az állványról a legegyszerűbben
gumival történő “kicsúzlizás” lehet. Ennek ereje akkora legyen, ami a
modellt a várható sebességre gyorsítja fel, tehát sem a túl kicsi, sem a
túl nagy indító erő - és sebesség - nem jó a mérésekhez. Ezt a mérések
előtti próbálkozásokkal kell megállapítani, azután mindig ezzel az erővel
kell az indításokat elvégezni.
A bevezetőben említett
könyvben - A modellrepülés elmélete - leírt siklóméréseket Benedek György
végezte a műegyetem aulájában, 1943-44. években. Az akkori mérések célja
volt azt megállapítani, hogy mennyit javít a turbószál egy vastag profilú
modell merülésén, és eldönteni azt hogy egy vékony szárnyszelvény vagy
pedig a vastag, turbószállal ellátott profil ad-e kedvezőbb eredményeket a
kisméretű repülőmodelleknél.
A kísérlethez külön
siklómodellt épített három szárnnyal, Gött. 625, N-60 és B 3357-b
szárnyszelvényekkel.

x |
0 |
1,25 |
2,5 |
5 |
7,5 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
95 |
100 |
% |
yf |
5,5 |
9,0 |
10,9 |
13,3 |
14,95 |
16,35 |
19,30 |
20,0 |
19,05 |
17,35 |
15,05 |
12,1 |
8,6 |
4,75 |
2,75 |
0,65 |
% |
ya |
5,5 |
3,3 |
2,35 |
1,25 |
0,75 |
0,4 |
0,1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
% |

x |
0 |
1,25 |
2,5 |
5 |
7,5 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
95 |
100 |
% |
yf |
3,4 |
5,6 |
3,76 |
8,24 |
9,33 |
10,14 |
11,98 |
12,44 |
12,03 |
11,06 |
9,55 |
7,66 |
5,5 |
3,04 |
1,72 |
0,40 |
% |
ya |
3,4 |
1,91 |
1,16 |
0,96 |
0,62 |
0,4 |
0,04 |
0,04 |
0,12 |
0,48 |
0,71 |
0,78 |
0,64 |
0,37 |
0,19 |
0 |
% |

x |
0 |
1,25 |
2,5 |
5 |
7,5 |
10 |
15 |
20 |
25 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
% |
yf |
0,4 |
1,61 |
2,45 |
3,78 |
4,83 |
5,68 |
6,98 |
7,8 |
8,29 |
8,58 |
8,55 |
8,07 |
7,03 |
5,65 |
4,0 |
2,12 |
0,15 |
% |
ya |
0,4 |
0,22 |
0,59 |
1,47 |
2,25 |
2,91 |
4,03 |
4,82 |
5,38 |
5,67 |
5,82 |
5,64 |
4,97 |
3,98 |
2,75 |
1,42 |
0 |
% |
|
A
modell adatai:
|
fesztáv:
61 cm.
törzshossz: 50 cm.
szárnyfelület 4,66 dm2
oldalviszony: 1 : 8
|
|
|
A felületi
terhelés:
|
Gött.
625 szárnynál
N-60 szárnynál:
B-3357-b szárnynál :
|
1,18 g/dm2
0,92 g/dm2
0,815 g/dm2
|
A táblázatban használt jelölések:
v = vízszintes sebesség
m/s - ban
w = merülősebesség m/s - ban
e = a siklószám reciproka
Cf = felhajtóerő tényező
Ce = ellenállás tényező
Re = abszolút sebességgel adódó Reynolds szám
Első mérés: Gött. 625 szárnyszelvénnyel:
|
Eredmények
|
v
|
w
|
e
|
Cf
|
Ce
|
Re
|
|
Turbószál
nélkül
|
5,1
|
2,7
|
1,9
|
0,725
|
0,382
|
83.000
|
|
Turbószállal
|
5,7
|
1,16
|
4,9
|
0,58
|
0,119
|
32.000
|
A turbószál nélküli
repülésnél feltűnően rosszak az eredmények. A modell nem is egészen 1:2
siklószámmal és közel 3 m/s merülő sebességgel valóságosan zuhan. (Félni lehetett
attól hogy a sok zuhanást a modell sérülés nélkül nem is bírja ki.)
Turbószál használatával
a helyzet szemmel láthatóan javult, a siklószám 1:5 - nek, a merülősebesség
pedig 1,2 m/s - nak adódott.
Kétségtelen hogy ezek az
eredmények gyengék, ez a vastag szelvény szabadonrepülő modellekhez nem
használható, a turbószál kedvező hatásának bemutatásához azonban ez a
kísérlet kiváló.
Második mérés: N-60
szelvénnyel
A mérések többféle
állásszöggel történtek.
A mérésnél feltüntetett
szögek nem a tényleges állásszöget jelentik, hanem a szárnyszelvény alsó
érintője és a vízszintes csillapító által bezárt szöget. A
szárnyszelvénynek a tényleges sebességgel bezárt szöge ismeretlen, mert az
a modellnek a levegőben való elhelyezkedése szerint alakul, egyáltalán nem
biztos hogy a repülőmodell a törzs hosszengelye irányában mozog, vagy hogy
vízszintes csillapító felület 0 fokos állásszöggel repül.
|
Eredmények
|
v
|
w
|
e
|
Cf
|
Ce
|
Re
|
|
Turbószál
nélkül 0 fok állásszög
|
5,54
|
1,08
|
5,1
|
0,48
|
0,094
|
32.200
|
|
Turbószállal
0°
|
5,0
|
0,715
|
7
|
0,59
|
0,084
|
28.600
|
|
1,8°
|
4,5
|
0,66
|
6,8
|
0,72
|
0,106
|
26.800
|
|
2,5°
|
4,22
|
0,61
|
6,9
|
0,826
|
0,118
|
24.200
|
|
6°
|
4,16
|
0,61
|
6,8
|
0,855
|
0,126
|
23.800
|
Az eredmények érdekese,
a turbószál jelentősen javítja a repülőtulajdonságokat, 0 fokos
állásszögnél a siklószám javulás kb. 27%-os, a merülősebesség csökkenése
30%, a minimális (0,61 m/s) merülősebességet véve alapul pedig a javulás
kb. 44%.
Kis Re számoknál tehát
az N-60-as vagy hasonló szelvény turbószállal felszerelve sikeresen
alkalmazható.
Ezek az eredmények
teljesen indokolttá teszik a turbószál használatát. Ugyancsak figyelemre
méltó hogy a süllyedő sebesség minimuma nagyobb állásszögeknél lép fel.
Megjegyzendő azonban hogy a 6 fokos állásszögnél már stabilitási nehézségek
mutatkoztak.
Harmadik mérés:
B-3357-b szelvény
Ez a mérés-sorozat azt
akarta eldönteni hogy a vastag szelvény turbószállal, vagy pedig egy
vékony, ívelt profil ad-e jobb sikló tulajdonságokat.
|
Eredmények
|
v
|
w
|
e
|
Cf
|
Ce
|
Re
|
|
Turbószál
nélkül
|
|
|
|
|
|
|
|
1,8°
|
4,3
|
0,60
|
7,2
|
0,71
|
0,099
|
24.800
|
|
3°
|
4,05
|
0,56
|
7,2
|
0,80
|
0,111
|
23.400
|
|
6°
|
3,57
|
0,51
|
7
|
1,03
|
0,147
|
20.600
|
Ezeket az eredményeket
az N-60-as mérésekkel összehasonlítva láthatjuk hogy a B-3357-b kedvezőbb.
Legjobb a helyzet 6 fokos állásszögnél, itt 1:7-es siklószámot és kb. 50
cm/s-os merülő sebességet sikerült elérni., ami ilyen kis Re számoknál kiváló
érték
A negyedik mérésnél
feladat volt annak megállapítása hogy milyen vastag legyen a turbó szál a
kellő turbulencia előidézéséhez
Ezek a mérések N-60-as
szelvénnyel történtek, de különféle átmérőjű turbószálakkal. A turbó szálnak
is lehet kritikus Re száma, amely alatt használata már eredménytelen.
A turbószál Re száma:
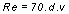
ahol
d = a szál átmérője mm-ben,
v = a sebesség m/s-ban
Amikor az alkalmazott
turbószál Re száma 300 volt, kifogástalanul működött, Re = 104-nél a hatás
már bizonytalanul jelentkezett, s végül Re = 49-nél a turbószál már semmi
javulást sem hozott.
Ha tehát olyan
turbószálat alkalmazunk, amelynek Re száma legalább 300, egészen bizonyos
hogy a határréteget turbulenssé tudja tenni. Mivel a mai modellek minimális
siklósebessége 4,5 - 5 m/s körül mozog, a szükséges turbószál átmérője:
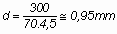 -nek
adódik. -nek
adódik.
Ennél vastagabb
turbószál használata nemhogy nem ad jobb eredményt, de csak felesleges
ellenállás
Repülőmodellek siklóteljesítményének
számítása.
Modelltervezés
alkalmával hasznos dolog néhány egyszerű számítást végezni a modell
teljesítményére vonatkozólag, hogy lássuk mit is várhatunk tulajdonképpen
repülőmodellünktől. A számítások segítségével némi tájékoztatást nyerhetünk
a szárny és a csillapító felület szögállására is.
A/2 típusú vitorlázó
modellt tervezünk. Az ezidőszerinti előírásnak megfelelően az összes
vízszintes felület 32-34 dm2 között lehet, mi érthetően a felső
határt választjuk. Legyen a csillapító felülete 4 dm2, a szárnyé
30 dm2 A gép tömege az FAI előírásai szerint 410 g lesz. A
felületi terhelés így
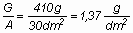
A szárny oldalviszonya
legyen
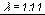
Szárnyszelvénynek
válasszuk a NACA-4409 jelű profilt. (Ennél alkalmasabb szelvény is akad
profilgyűjteményünkben, de a számításokat a 4409-es-sel végezhetjük el
legmegbízhatóbban, mert ennek szélcsatorna-mérései állnak
rendelkezésünkre.)
A számításoknál a
szárnyat tiszta téglalapnak tekintjük és az indukált ellenállás, valamint
az állásszög-számításoknál a Glauert-féle korrekciós értékeket használjuk.
Mint láttuk a szárny
alaprajzi formájának az indukált ellenállásra csak csekély, elhanyagolható
befolyása van, s így a szárnyat bármilyen alaprajz szerint készíthetjük.
A szárny Re számának
kiszámításához ismernünk kell a szárnyszelvény hosszát. A felvett adatokból
ezt kiszámíthatjuk. A szárny fesztávolságát “b” - vel, a szelvény hosszát
“a”- val jelölve:
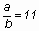 és és 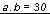 dm2 dm2
e két egyenletből:
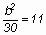
ebből
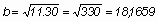 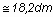 =
1820 mm =
1820 mm
A szárnyszelvény hossza
így:
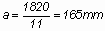
A számításnál különféle
Cf értékeket veszünk fel és minden esetben kiszámítjuk a modell vízszintes
sebességét, Reynolds számát és indukált ellenállását.
A modell szelvénye szerinti
táblázatból vagy diagramból a Reynolds számnak megfelelően leolvashatjuk a
végtelen oldalviszonyú szárny ellenállás tényezőjét, ez a tiszta
profil-ellenállás. (Cepr)
A modell összes többi alkatrészének
káros ellenállását az ismertetett siklómérések alapján tudjuk megbecsülni,
ez legyen 0,025
A profil, - indukált, -
és káros ellenállások összege adja a modell összes káros ellenállását, a Ceö
- t, a modell teljes ellenállás—tényezőjét
Az előre felvett Cf
értékek és a kiszámított Ceö összes ellenállás tényező hányadosa megadja a
modell siklószámának reciprokát, az e - t. A vízszintes sebesség
osztva az e - nal pedig a merülősebességet mutatja. Az összes
adatot táblázatosan leírva rögtön szembetűnik hogy milyen
felhajtóerő-tényezőnél áll be a legkisebb merülés.
A táblázat
kiszámításához használt képletek:
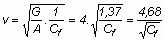
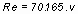
Az indukált ellenállás
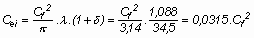
Az indukált ellenállás
kiszámításához használt “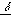 ”
tényező értékét 1:11 oldalviszonyú téglalap szárny esetére táblázatból
(Glauert-féle táblázat) találjuk meg. Ugyanebből a táblázatból vesszük a
téglalap szárny indukált állásszögének számításához használt ”
tényező értékét 1:11 oldalviszonyú téglalap szárny esetére táblázatból
(Glauert-féle táblázat) találjuk meg. Ugyanebből a táblázatból vesszük a
téglalap szárny indukált állásszögének számításához használt 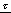 = 0,24 tényező értékét is: = 0,24 tényező értékét is:
|
l
|
1:5
|
1:6
|
1:7
|
1:8
|
1:9
|
1:10
|
1:11
|
|
d
|
0,037
|
0,046
|
0,055
|
0,064
|
0,072
|
0,080
|
0,088
|
|
t
|
0,145
|
0,163
|
0,183
|
0,201
|
0,216
|
0,228
|
0,240
|
|
Cf
|
v m/s
|
Re
|
Cepr
|
Cei
|
Cek
|
Ceö
|
e
|
w m/s
|
|
0,4
|
7,4
|
85.500
|
0,015
|
0,005
|
0,025
|
0,045
|
8,9
|
0,83
|
|
0,5
|
6,6
|
76.300
|
0,013
|
0,008
|
0,025
|
0,046
|
10,9
|
0,61
|
|
0,6
|
6,0
|
69.400
|
0,015
|
0,011
|
0,025
|
0,051
|
11,8
|
0,51
|
|
0,7
|
5,6
|
64.800
|
0,015
|
0,015
|
0,025
|
0,055
|
12,7
|
0,44
|
|
0,8
|
5,2
|
60.000
|
0,017
|
0,020
|
0,025
|
0,062
|
12,9
|
0,40
|
|
0,9
|
4,9
|
56.600
|
0,021
|
0,025
|
0,025
|
0,071
|
12,7
|
0,39
|
|
1,0
|
4,7
|
54.300
|
0,030
|
0,032
|
0,025
|
0,087
|
11,5
|
0,41
|
|
1,1
|
4,5
|
52.000
|
0,045
|
0,038
|
0,025
|
0,108
|
10,2
|
0,44
|
Bár a minimális 0,39 m/s
- os merülősebesség igen csábító, a gyakorlat azt mutatta hogy nagy Cf
értékeknél, - tehát nagy szárny-állásszög esetén - a modell hosszanti
egyensúlya már bizonytalan. A gyakorlati tapasztalatoknak megfelelően ezért
inkább kisebb felhajtóerő-tényezőnél érdemes maradni, mint amilyent a
minimális merülősebesség adna. A jelen esetben megfelelő a cf =
0,7 - 0,8-as érték, ahol a merülés 0,44 - 0,40 m/s - nak adódik.
Nézzük meg, hogy cf
= 0,8 es felhajtóerő eléréséhez milyen szárny-állásszöget kellene
alkalmaznunk. NACA 4409-es szelvény adatai között megtalálhatjuk a Cf = 0,8
- hoz tartozó állásszöget végtelen oldalviszony esetén, ez kb. 3,7 fok.
A 11-es oldalviszonyú
téglalap-szárny miatt fellépő indukált állásszög:
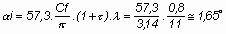
Ez azt jelenti hogy a
szárny mögött fellépő leáramlás iránya kb. 1° 40’ a vízszinteshez képest. Ha
azt akarjuk hogy a csillapító felület 0° - os állásszöggel kapja az
áramlást, akkor a törzs hossztengelyéhez képest +1° 40’ - es szögállást kell adnunk.
Ugyanekkor a szárny teljes
állásszöge az indukált állásszög és profil-állásszög összege, tehát a i + a a jelen esetben 1,65° + 3,7° = 5,35° @ 5° 20’ a törzs hossztengelyéhez
képest.
A csillapítófelület és a
szárny síkjai által bezárt szög azonban csak 3,7° , azaz kb. 3° 40’. Ezzel a beállítással kell
megkezdenünk a modell berepítését és a súlypontot olyan helyzetbe hoznunk,
amelynél a modell hosszanti egyensúlya kielégítő.
Sajnos nem bizonyos,
hogy a modell a számított szárny és csillapító állásszögeknek megfelelően
fog siklás alkalmával a levegőben elhelyezkedni, ezért a súlypont helyzetét
változtatni és szükség esetén a beállított állásszögeket korrigálni kell.
Az eddigi tapasztalatok után legcélszerűbbnek látszik a modell
siklósebesség szerinti beállítása.
A most számolt A/2 - es
vitorlázó modell vízszintes sebessége kb. 5,2 m/s kell legyen. A számolt
állásszögeket alkalmazva addig változtatjuk a súlypont helyzetét, amíg az
5,2 m!s sebességet elérjük. Ha ez a súlypont helyzetének tologatásával nem
sikerülne, csak akkor változtatunk az állásszögeken. Fixen beépített szárny
és csillapító esetén természetesen csak a súlypont helyzetének
állítgatásával tudunk segíteni.
A modell merülősebessége
0,4 m/s - nak adódik. Nézzük meg most hogy a jelenlegi FAI előírás szerint
az A-2 - es modellekre előírt 50 m - es zsinórral felhúzva milyen
időtartamot képes repülni álló, est levegőben.
Feltételezzük hogy a
modellt 50 m magasan tudjuk leoldani. Az 50 m magasságból elérhető
időtartam:
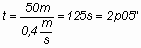
Álló levegőben ilyen
modellnél ez egészen reális érték.
Bármilyen más típusú,
szabadonrepülő modell siklóteljesítményét hasonló közelítő számítással
tudjuk meghatározni.
<< előző rész
| következő rész >>
|