SÚLYPONTSZÁMÍTÁS
REPÜLŐGÉPMODELLEKRE
(KIEGÉSZÍTÉS)
A Súlypontszámítás Repülőmodellekre című archivált írás vagy eredetileg is zavaros lehetett, vagy a fordítók követtek el egy-két hibát, de biztos, hogy az értékes szakmai anyagot nagyon nehezen értelmezhető formába öntötték. Ennek talán az lehet az oka, hogy keverték a valódi repülőgépeknél és a repülőgépmodelleknél használatos szakkifejezéseket, valamint a számítási eljárást nem logikai sorrendben ismertették.
Nem szoktam archivált cikkekhez értelmezést hozzáfűzni, de ebben az esetben ezt szükségesnek látom, mivel maga a számítási eljárás nagyon hasznos és megismerése, alkalmazása komoly segítséget jelent, mint a modelltervezés elméleti kérdéseinek megoldásában, mint a kész modellek beállításában. Ez a kiegészítés önmagában használható, de érdemes elolvasni az eredeti cikket is.
Alapfogalmak
|
Fesztávolság |
A modell szárnyának két legszélső pontját összekötő, a hossztengelyre merőleges vonal hossza, más néven szárnyterjedtség. |
|
Közepes aerodinamikai húrhossz |
KAH. Ez a szárny azon húrhossza, amellyel azonos terjedtségű, téglalap alakú szárnyat készítve, az eredetivel megegyező aerodinamikai tulajdonságokkal bíró szárnyat kapnánk. |
|
Nyomásközéppont |
A modellre ható légerők eredőjének támadáspontja, más néven semleges pont. |
|
Oldalviszony |
A repülőgépszárny aerodinamikai sajátosságát befolyásoló tényező. dimenzió nélküli szám. A fesztávolság és a közepes aerodinamikai húrhossz arányát fejezi ki. |
|
Semleges Pont |
A modellre ható légerők eredőjének támadáspontja, más néven nyomásközéppont. |
|
Súlypont |
A repülőgépmodellre ható súlyerők eredőjének támadáspontja, másként tömegközéppont. |
|
Szárnymélység |
A szárny egy adott pontján a hossztengellyel párhuzamos szárnymetszet hossza. |
Az elemi szárny
nyomásközéppontjának és közepes aerodinamikai húrjának meghatározása
A számítási eljárás alapja, hogy a repülőgépmodellt egyes jól elkülöníthető felületekre osztjuk fel. Az egyes felületeknek meghatározzuk a semleges pontját, és a felület nagyságát. Ezen két adat ismeretében egy viszonyítási vonaltól (tengelytől) kiszámoljuk a felület nyomatékát. A nyomatékokat összegezzük, és a kapott adatokkal a véges szárny elmélet megkövetelte korrekciókat elvégezzük. Így kapjuk meg a gép semleges pontját. Ennek ismeretében különféle stabilitási mértékekhez tartozó súlyponthelyzetek is meghatározhatóak.
Az eljárás alapja a szárnyfelület semleges pontjának és közepes aerodinamikai húrjának meghatározása.
Az elemi szárny (felület) semleges pontjának meghatározása grafikus módon az alábbi ábra szerinti módon történik.
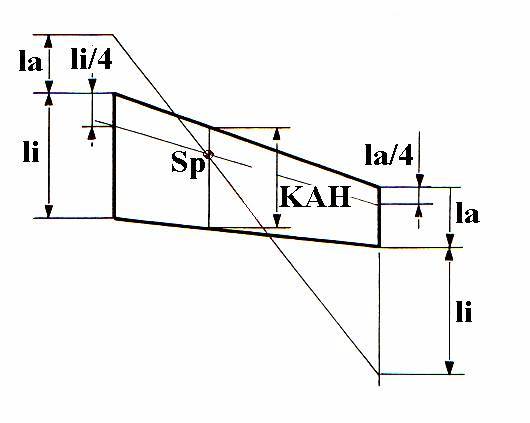
1.ábra.
Ahol li a szárnymélység belül, la a szárnymélység kívül Sp a semleges pont helye, KAH a közepes aerodinamikai húr hossza. Mint látható a semleges pont szerkesztéssel való meghatározása elemi szárnyon igen egyszerű feladat. Az eredmény pontosságát nagymértékbe befolyásolja a méret amiben a rajzot készítjük, valamint a szerkesztés pontossága.
Számítási példa
A számítás folyamatát a legegyszerűbben egy példán keresztül lehet megérteni. Alkalmazzuk a műveletsort a sokak által ismert AND NOW típusú repülőgépmodellre. Rajzoljuk meg a repülőgépmodell felülnézeti képét.
Először egy viszonyítási vonalat kell megválasztanunk, ami derékszögű a törzs középvonalára. A viszonyítási vonal legyen célszerűen a szárny belépőéle.
A szárny
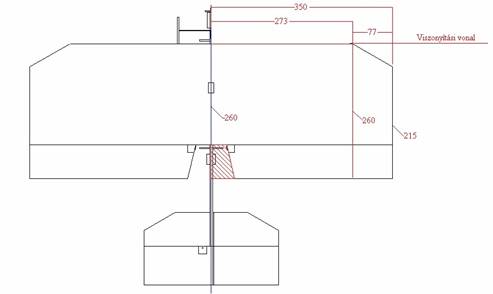
2. ábra.
Vegyük fel a méreteket. A szárny két részre osztható. A téglalap alakú szárnytőre, és a trapéz alakú szárnyvégre. A szárny méreteibe természetesen beletartoznak a csűrőlapok is. A szárny hátsó részén a törzs mellett a csűrőlapok nem érik el a törzs vonalát. Ezt a kivágást a számítások során elhanyagoljuk, úgy vesszük, mintha a szárny itt is anyagfolytonos lenne (bevonalkázott terület)
Húrhossz a tőben: l1=260 mm
Húrhossz a belső szárnyrész végén: l2=260 mm
Húrhossz a külső szárnyrész végén: l3=215 mm
Belső szárnyrész fél-fesztávja: b1=273 mm
Külső szárnyrész fél-fesztávja: b2=77 mm
Teljes szárny fél-fesztávja: b=350 mm
Határozzuk meg a belső szárnyrész felületét és semleges pontjának a helyét.

3. ábra
Egyszerű feladatunk van, mivel a belső szárnyrész téglalap alakú, tehát az ¼-ed húrhossz vonala párhuzamos a belépőéllel és derékszögű a törzs tengelyére. Az Sp1 pont pedig a szárnyrész felénél van.
Az Sp1 pont távolsága a viszonyítási vonaltól: x1= 260/4 = 65 mm
A szárnyrész felülete: F1=l1*b1=260*273=70980 mm2
Határozzuk meg a külső szárnyrész felületét és semleges pontjának a helyét.
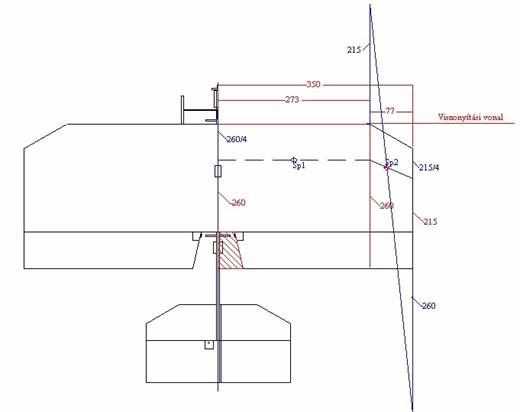
4.ábra
Itt már nehezebb dolgunk van, mivel a külső szárnyrész trapéz alakú. A szárnyrészre alkalmazzuk az 1. ábrán látható szerkesztési módszert. A szárrész tövében és végén mérjük fel az ¼ húrhosszakat és az így kapott pontokat kössük össze. Ezt követően a szárnyrész tövében előre mérjük fel a szárnyrész végének húrhosszát (215 mm) a szárnyrész végében pedig mérjük fel a tő húrhosszát hátrafelé (260mm) az így kapott pontokat is kössük össze. A két vonal metszéspontja adja a szárnyrész semleges pontját. (Sp2). Ezen pont távolságát mérjük meg a viszonyítási vonaltól. A szárnyrész felületét a geometriából ismert, trapézokra alkalmazható, felületszámítási képlet segítségével határozzuk meg.
Az Sp2 pont távolsága a viszonyítási vonaltól: x2=78,9 mm
A külső szárnyrész felülete: F2=((l2+l3)/2)*b2=(260+215)/2)*77=18287,5 mm2
A két szárnyrész adatait összegezzük:
Félszárny teljes felülete : F=F1+F2=70980 + 18287,5 = 89267.5 mm2
Semleges pont helye: Sp=((F1*x1)+(f2*x2))/F
= ((70980*65)+(18287,5*78,9))/89267.5=67,847 mm
Közepes szárnymélység lm=((l1+l2)*F1)+((l2+l3)*F2)
/ (2 * F) =((260+260)*70980)+((260+215)*18287,5) / (2*89267)= 255,39 mm
Oldalviszony L=
(2*b)/lm = (2*350)/255,39= 2,74
A vízszintes
csillapító
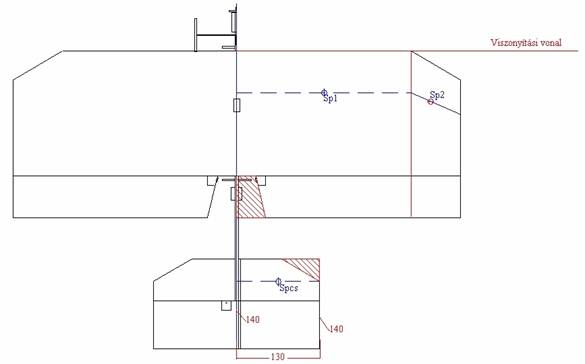
5.ábra
A vízszintes csillapító számításait egyszerűsítendő, a csillapító belépőélének levágását elhanyagoljuk, és úgy tekintjük mintha a felület téglalap alakú lenne (bevonalkázott terület)
A vízszintes csillapító állandó húrhossza: lcs=140 mm
A vízszintes csillapító fél fesztávja: bcs=130 mm
A felület semleges pontjának és nagyságának meghatározása itt is igen egyszerű, mivel téglalap alakú felülettel van dolgunk.
A csillapító semleges pontjának távolsága a viszonyítási vonaltól xcs= Spcs = 360 mm
Vízszintes csillapító felének felület Fcs=lcs * bcs = 140 * 130 = 18200 mm2
Vízszintes csillapító közepes húrhossza : lmcs = Lcs = 140 mm
Oldalviszony: Lcs= (2*bcs)/lmcs = (2*130) / 140 = 1,8571
A vízszintes csillapító erőkarja a szárny semleges pontja és a csillapító semleges pontja közötti távolság. Mindkét semleges pontot a viszonyítási vonalhoz képest határoztuk meg így egy egyszerú kivonással ezt az értéket is megkapjuk
Csillapító erőkarja Rcs= Spcs –Sp = 360- 67,847 = 292,153 mm
Képletek
behelyettesítése
Az adatfelvételekkel, és az előzetes számításokkal végeztünk. A kapott eredményeket ellenőrizzük le mégegyszer, majd nekikezdhetünk a stabilitási számításoknak.
1.) A szárny okozta leáramlás hatása. δε/δα= 4/(L+2) = 4/(2,74+2) = 0,84388
2.) A szárny felhajtóerő növekedése: CAα = (2* π *L) /(L+2)=(2 * π * 2,74) / (2,74+2) =
3,6319
3.) Vízszintes csillapító volumen : Vcs= (Fcs * Rcs) / ( F* lm) = (18200 * 292,153) / (89267,5 * 255,39) =
0,23323
4.) Vízszintes csillapító bólintó nyomatékának növekedése
CMαcs= (-0,9 * Vcs * Lcs * π)
/(1+ √(1+(Lcs:2)2) = (-0,9*0,23323*1,8571*π)/(1+√(1+(1,8571:2)2))=-0,517889
5.) A semleges pont relatív helyzetének mérőszáma : γN= (0,25- CMαcs) /( CAα * (δε/δα)) = (0,25-(-0,517889))/(3,6319*0,84388)=0,2505439
6.) A semleges pont helye a közepes szárnymélységre
vonatkoztatva lm*
γN=255,39*0,2505439=63,986 mm
A kapott adatok
értelmezése:
Először szerkesztéssel határozzuk meg a gép semleges pontját, és a lehetséges súlypont helyzeteket
Rajzoljuk fel a szárny semleges pontját(SPsz), (belépő éltől 67,847 mm). A közepes szárnymélység (lm) ¼-ed részét mérjük fel a szárny semleges pontja elé (lm/4=63,847 mm), majd az így kapott ponttól hátrafelé mérjük fel a közepes szárnymélységet (lm=255,39). Ezzel gyakorlatilag kiszerkesztettük az eredetivel aerodinamikailag egyenértékű téglalap szárnyat.
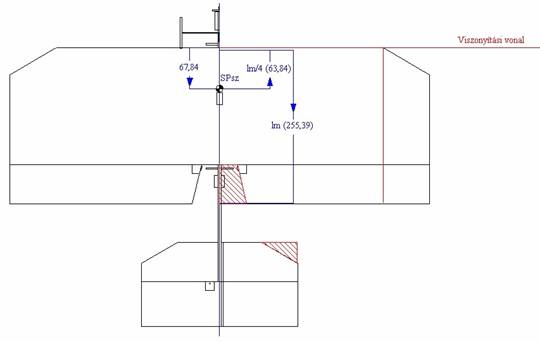
6.ábra
Az egyenértékű szárny belépőélétől mérjük fel lm* γN értékét (63,986 mm) és megkapjuk a teljes gép semleges pontjának a helyét (SPg). Ez előtt a semleges pont előtt a közepes szárnymélység 8…10 %-ával (vagy kisebb értékkel) kell elhelyezkednie a modell súlypontjának (CG). Ezt is rajzoljuk fel az ábrára. A kapott két
pont távolságát mérjük le a valós szárny belépőélétől:

7.ábra
A gép semleges pontjának távolsága a belépőéltől: Xspg = 67,9 mm
A 10%-hoz tartozó (szélső) súlyponthelyzet a belépőéltől: XCG10%= 42,4 mm
Ugyanezen adatokat egyszerűbben és pontosabban is meghatározhatjuk számításos eljárással:
Viszonyítási vonalnak most vegyük fel a valós szárny belépőélét, ha a szárny nyilazott akkor a szárny-törzs csatlakozás pontjában a törzs vonalára merőleges egyenest. Ez lesz a „0” vonal.
A gép semleges pontjának helye a „0” vonaltól (valós szárny
belépőélétől): Xspg= (Sp-(lm/4))+ lm*
γN = (67,847-(255,39/4))+63,986 =
67,9855 mm
A gép 10%-hoz tartozó szélső súlyponthelyzete a „0” vonaltól
(valós szárny belépőélétől): XCG10%=
Xspg-(lm*0,1)=67,9855-(255,39*0,1)= 42,4465 mm
A kapott
eredmények összegzése.
A számítások révén kapott adathalmaz gyakorlati hasznosításához (pl.: reptetés előtti beállítások elvégzése) érdemes az eredményeket egységes táblázatba foglalni. Ezt a táblázatot mellékelhetjük a repülőgépmodell dokumentációjához, és a további fejlesztések, beállítások során a gyakorlatban kapott adatokkal kiegészíthetjük. Így repülőgépmodellünk aerodinamikai tulajdonságait jól leíró adattárra tehetünk szert.
|
Megnevezés: AND NOW |
|
|
Jelleg |
Slowflyer |
|
|
|
|
Szárnyfelület |
17,853 dm2 |
|
Vízszintes csillapító felülete |
3,64 dm2 |
|
Teljes hordfelület |
21,49 dm2 |
|
Repkész tömeg: |
266 gramm |
|
Felületi terhelés |
12,37 g/dm2 |
|
Gép semleges pontja a szárny belépőéltől: |
67,98 mm |
|
10% lm –hez tartozó, szélső, súlyponthelyzet a belépőéltől: |
42,44 mm |
|
Stabilitási adatok: |
|
|
Stabilitás mértéke % |
Súlypont a belépőéltől: |
|
0 |
67,98 mm |
|
2 |
62,87 mm |
|
4 |
57,76 mm |
|
6 |
52,65 mm |
|
8 |
47,54 mm |
|
10 |
42,44 mm |
Az And Now eredeti leírásában a súlyponthelyzetet a belépőéltől 65 mm-re adta meg a tervező. Ez 1,16%-os relatív stabilitási értéknek felel meg. A gép tervezője egy fordulékony beállítást javasol ezzel az értékkel. A stabilitási adatokból megállapítható, hogy a berepítésnél nyugodtan beállíthatunk akár 50-55 mm súlyponttávolságot is a belépőéltől, és ezzel egy nagyon stabil, nyugodt tulajdonságokat mutató gépet fogunk kapni. Majd ahogy kiismerjük a gép repülési jellemzőit, illetőleg elvégeztük a pontos trimmelés, hátrább vihetjük a sülypontot egészen 65…67 mm-ig ahol kihasználhatjuk az „idegesebb” jellemzők adta könnyű műrepülhetőséget.
♣ SRY MODELL ♣
2005 ♣ Powered by MS WORD ♣ IMSI Turbo CAD ♣
♣ 2005. július 26.
♣