---

---

Eredeti megjelent:

Modellezés

1992. I.szám 20-21. old.

Súlypontszámítás repülőmodellekre

Német laptársunkban megjelent tanulmányában Frederik Lanchen érdekes számításokat közöl súlypontszámításhoz. Írásában D.Altenkirch, valódi gépekhez készített képleteit használja fel.

A következőkben ismertetünk egy egyszerű, de elegendően pontos eljárást a modell semleges pontjának (nyomásközéppontjának) meghatározásához. A semleges pont ismerete előfeltétel a súlypont kiszámításához.

E súlyponthoz viszonyított távolsága adja meg a stabilitás mértékét. Helyzete független az alkalmazott profiltól; kizárólag könnyen meghatározható geometriai adatokat kell figyelembe venni. Ez biztonságot nyújt a berepítéskor, mivel a súlypont helyzetét már nem kell becsülni. Még a későbbi, gyakran hosszadalmas "besúlyozás" is elmaradhat, ha pontosan elvégezzük a következő méréseket és számításokat.

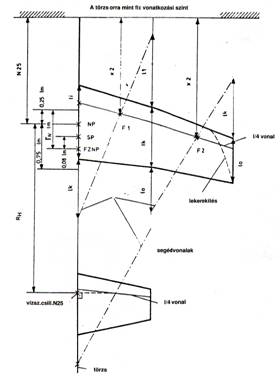
1.ábra.

(az ábra rákattintva nagy méretbe, új ablakban megjeleníthető)

SZÁMÍTÁSI ELJÁRÁS

(lásd az ábrát) Először elkészítjük a modell felülnézeti rajzát papíron 1:10-es arányban. Ehhez a következő méreteket kell dm-ben meghatározni, amilyen pontosan csak lehetséges, közvetlenül a modellen végzett mérésekkel. (A későbbi számításokban négy tizedesnyi pontossággal dolgozzunk, hogy a hibát elfogadható határok között tarthassuk.)

b - teljes fesztávolság (a törzs hossztengelyére merőlegesen)

l_i - szárnymélység, belül

l_a - szárnymélység, kívül

l_k - szárnymélység

b₁, b₂ - rész fesztávolságok

EGYSZERŰSÍTÉSEK

- A derékszögű, téglalap alakú szárny esetében elmarad a közepes szárnymélység, kiszámítása, mivel ez azonos a szárnytő mélységével.

- Ha a téglalapszárny nem nyilazott, úgy a szárny semleges pontja a szárnytő mélységének 25%-ában van.

- Egyszerű trapézszárny esetében l_a, b₂, x₂ nem értelmezhető, értékük nulla.

- Amennyiben az 1/4 vonal a teljes fesztávolságon át merőlegesen fut, a törzs hossztengelyére, úgy a szárny semleges pontja a szárnytő mélységének 25%-ában helyezkedik el.

- Ha a szárny alakja elliptikus vagy ehhez hasonló, akkor a szárnymélységet a fél fesztáv mentén integrálni kell.

A RÉSZFELÜLETEK SEMLEGES PONTJÁNAK MEGHATÁROZÁSA

Mérjük fel a mindenkori részfelület belső mélységét kívül, a külső mélységét pedig belül (ahogyan ez az ábrán látható). A segédvonalaknak az 1/4 vonallal adódó metszéspontjaiból adódnak a részfelületek semleges pontjai. Ezután megmérjük a részfelületek semleges pontjának távolságát (x₁, x₂) a törzsorrig (a bázisvonal az 1.ábrán), majd kiszámítjuk a részfelületeket:

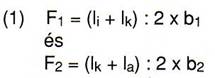
Eközben a szárnyat úgy számoljuk, mintha a vége lekerekítés nélküli, vagyis egyenes lenne.

A részfelület semleges pontokat a részfelületek arányának megfelelően kell súlyozni , hogy megkapjuk a szárny semleges pontját. Ha behelyettesítjük a fenti értékeket a

egyenletbe, megkapjuk a szárny semleges pontjának helyzetét. Ezt a pontot bejelöljük a törzsön illetve a szárnytövén (NSZ pont).

A közepes szárnymélység az összes szárnymélység számtani középarányosa és a következő egyenlettel számíthatjuk ki:

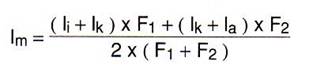
A közepes szárnymélység eleje (az "orrléc") 0,25 x l_m távolságra van a szárny Nsz semleges pontja előtt. A vége (a "kilépőléc") 0,75 x l_m-nél helyezkedik el a szárny semleges pontja mögött. Ezt a két pontot is bejelöljük a törzsön illetve a szárnytövén. Ugyanilyen módon szerkesztjük ki a vízszintes csillapítósík semleges pontjának (N_CS) helyét is (az orrlécet és a kilépőlécet itt nem kell megjelölni).

A vízszintes csillapítósík erőkarja (R_CS) a csillapító semleges pontja és a szárny semleges pontja közötti távolság. Kacsa modell esetében ezt a távolságot majd negatív előjellel kell a képletbe behelyettesíteni.

TOVÁBBI SZÁMÍTÁSOKHOZ SZÜKSÉGES ADATOK:

1.Szárnyfelület, F (dm2), Fesztáv x közepes szárnymélység

2.Közepes szárny mélység, lm (dm), (3) képlet

3.Szárny oldalviszony ,L (-), fesztáv/közepes szárnymélység

4.Vízszintes csill. FCS (dm2) analóg a szárnyfefelületlülettel

5.Vízszintes csill. Viszony, Lcs (-) analóg a szárny oldaloldlaviszonnyal

6.Csillapító erőkar, RCS (dm) lásd a szöveget

KÉPLETEK

A fenti adatokat helyettesítsük be az alábbi - minden külön magyarázat nélkül közölt - képletekbe és sorban számítsuk ki azokat.

Az irányértékek támpontként szolgálnak a közbenső eredmények nagyságrendjéhez.

A γ_N x 100 szorzat a semleges pont relatív helyzetét adja meg a közepes szárnymélység százalékában. A repülőmodell semleges pontja tehát l_m x γ_N távolságra helyezkedik el a törzsön berajzolt közepes szárnymélység belépő éle mögött.

A súlypont mintegy 8-10%-kel (az l_m-re vonatkoztatva) vagy ennél kevesebbel legyen a repülőmodell semleges pontja előtt. Semmi esetre sem lehet mögötte!!! Az SN távolság (pl. 8%) a stabilitásmértékét fejezi ki. PI. egy RC modell esetében. Minél közelebb van az S az N-hez, annál fordulékonyabb a modell a kereszttengely körül, de a csökkenő stabilitás miatt nehezebb vezetni. Ezért a magassági kormány kitérését csökkenteni kell, így a modell pumpáló mozgása kisebb lesz.

Ha az S az N közelében van, akkor a repülés pályájának a dőlésszöge közel állandó marad minden sebességnél. A modell viselkedése a kereszttengely körül közelítőleg indifferens.

Az archiváló megjegyzése: Igen nagy figyelemmel, és némi előképzettséggel, kell elolvasni a fenti cikket, ahhoz, hogy minden részletében értelmezhető legyen. Sajnos lényegi hibák is vannak benne (Pl. a 7. képlet Lcs tagja ami sehol máshol nem szerepel és a szöveg sem ad rá magyarázatot, hogy mi is lehet ez), és a számítások természetes logikai sorrendjét sem követi. Mivel ez egy igen hasznos és értékes szakmai anyag készítettem hozzá egy kiegészítést, aminek segítségével könnyebbé válik a fentiek megértése, és a közölt egyenletek valóban minden repülőmodellező hasznára lehetnek. A KIEGÉSZÍTÉS ITT>>> olvasható

(Kép és szöveg az FMT nyomán)

_{♣ Archiválta SRY 2005 július 12. ♣ CANON LiDE system ♣ Microsoft Word ♣ SRY MODELL 2005}