---

---

Eredeti megjelent:

Műszaki Könyvkiadó

Budapest 1980

33. old … 42. old.

Dr. Ordódy Márton

Sárkányrepülés (I.)

A kötet első 32 oldalán Dr. Ordody Márton áttekinti a sárkányrepülés történetét a kezdetektől, könyv kiadásáig, külön megemlékezve a magyar úttörőkről. Ezeket a részeket nem archiváltam, mivel a technikatörténeti értékek mellett lényeges műszaki információkat nem tartalmaznak.

I.	2. Mint a madár 2.1. A siklószárny mozgásai 2.2. A felhajtóerő keletkezése
II.	2.3. A siklás
III.	2.4. A forduló 2.5. Különleges repülési helyzetek 2.5.1. Átesésre visszavezethető repülési helyzetek
IV.	2.5.2. A vitorla átlobbanására visszavezethető repülési helyzetek
V.	2.6. Siklószárnyak teljesítménye

2.

Mint a madár

A motor nélküli, levegőnél nehezebb repülőszerkezetek repülése - akárcsak a madaraké - két erőtől függ: a Föld és a szárny tömege között ébredő kölcsönhatás eredményétől, a G súlyerőtől és a levegő és a szárny felülete közötti kölcsönhatásból származó R légerőtől. A kettő viszonya határozza meg a repülés pályáját. A repülő testet adott pályára kényszeríteni kormányzással lehet. A repülőgép vezetője merev kormánylapokkal, a madár egész testével kormányoz. A hajlékony szárny alakja, a vitorla formája a súlypont áthelyeződésének hatására megváltozik, a hajlékony szárny tehát ebből a szempontból a madárszerű repüléshez áll közelebb.

A repülőszerkezetek fontos tulajdonsága, hogy bizonyos határok között kormányzás nélkül, azaz önmagukban is képesek repülni. A repülőgépeknek ez a tulajdonsága a stabilitás. A sárkány az eddig ismert legegyszerűbb eszközökkel tesz eleget a kormányozhatóság és a stabilitás követelményeinek. A Rogallo-elv szerint ugyanis egyenes rudakból és síkba teríthető szövetből is lehet a levegőnél nehezebb, önmagában repülő szerkezetet építeni. A jelenleg épülő sárkányok tartói gyakran eltérnek az egyenestől, a vitorla is erősen szabott és merevített, a vitorlaszárnyra vonatkozó alapelvek azonban ma is érvényesek. Valószínű, hogy a hajlékony szárny tulajdonságainak alapos megismerésével egy sor, ma még felderítetlen lehetőség tárul fel. Azonban a vitorlaszárny is szárny, és akár a teljesítmény növelésének útjait keressük, akár pedig a repülő embert veszélyeztető kritikus helyzetekről van szó, a merevszárnyakkal kapcsolatban már ismert tények, eredmények felhasználása elengedhetetlen. A sárkány a hagyományos repülőgépek között farok nélküli, azaz csupaszárny-rnodellnek minősül. Hasznos tehát, ha a csupaszárny-repűlőgépekre vonatkozó régi ismeretek párosulnak a hajlékony szárnyra vonatkozó új ismeretekkel. Ez a fejezet alapfokon próbál ennek az igénynek eleget tenni.

2.1.

A siklószárny mozgásai

A repülőgépekbe a pilóta bele van szíjazva, ezért a pilóta együtt mozog a szerkezettel; mozgástani szempontból része a gépnek. A sárkányokon más a helyzet: a pilóta kormányzás közben a szárnyhoz képest változtatja helyzetét, vándorol tehát a szárny-pilóta egység közös súlypontja. Mivel a pilóta súlya az egység súlyának 60-80 %-át teszi ki, ezért a közös súlypont vándorlása jó közelítéssel követi a pilóta súlypontjának vándorlását A pilóta karján ébredő kormányerő és a felfüggesztő erő a szárny-pilóta egység szempontjából belső erő, tehát az együttes mozgást nem befolyásolja

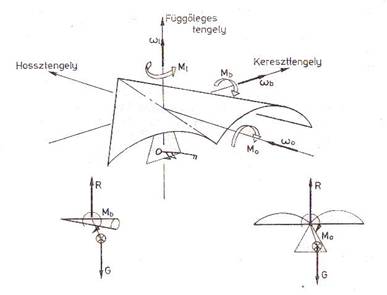
2.1.ábra.

A siklószárnyhoz kötött koordináta-rendszer

A siklószárny mozgásai közül különleges jelentőségű az állandósult siklás és az állandósult forduló esete. Mindkét esetben szokás a sebesség- és erőviszonyokat a szárnyhoz kötött megfigyelő, vagyis a pilóta szempontjából vizsgálni. A szárnyhoz kötött rendszerben a szárny-pilóta egység nyugalomban van, mindkét mozgás visszavezethető tehát az egységre ható erők egyensúlyára. A légerőt ilyenkor nem a szárny mozgásából, hanem a nyugalomban levő, de a haladási sebességnek megfelelően megfújt szárny áramlásmódosító hatásából lehet származtatni. Kormányzás hatására az állandósult mozgást végző szárnyhoz kötött rendszerben az egyensúly megbomlik, és átmeneti mozgás során újabb egyensúly, élesebb forduló vagy meredekebb szögű siklás jön létre. Az a kismértékű kormánymozdulat, amely során a pilóta az állandósult mozgáshoz tartozó testhelyzetből rövid időre kimozdul, az egyensúly megzavarása. Akkor is zavarásról beszélünk, ha az állandósult mozgást széllökés befolyásolja. Ha a zavarás megszűntével a szárny rövid átmeneti mozgás során magától az előző állandósult mozgásra törekszik, akkor a szárny stabil, ellenkező esetben pedig nem.

A mozgások vizsgálatához szokás három tengelyből álló koordinátarendszert kötni a szárnyhoz (2.1. ábra). A kereszttengely körüli forgás az ún. bólintó mozgás, amelyet a pilóta testsúlyának előre-hátra helyezésével hoz létre. Például a testsúly hátrahelyezésével mindaddig, míg az új állandósult siklóhelyzet létre nem jön, a légerő a szárnyat a súlypont körül M_b bólintónyomatékkal forgatja. A hossztengely körül a szárny orsózó mozgást végez, ennek előidézéséhez a pilóta a kormányrúd mentén jobbra balra helyezkedik. Amíg a súlyerő és a légerő újra egyensúlyba nem kerül, a súlyponton kívül ható légerő M_o orsózónyomatékkal forgatja a szárnyat. A függőleges tengely körüli legyező mozgáshoz az M_l legyezőnyomatékot a két félszárnyon nem azonos módon megoszló légerők keltik. A pilóta pusztán súlyáthelyezéssel - kormányfelületek híján - tiszta legyező mozgást nem is képes előidézni; a függőleges tengely körüli elfordulást tehát a szárny egyéb mozgásai váltják ki.

2.2.

A felhajtóerő keletkezése

Zárjuk össze ujjainkat és tartsuk nyitott tenyerünket a robogó jármű ablakából a szélbe! Amíg a tenyér élével halad a szél ellen, addig csak enyhe hátrahúzó erőt érzünk. Tenyerüket enyhén elfordítva a hátrahúzó erő mellett hirtelen erős emelő hatás jelentkezik. További elfordítás hatására a felfelé húzó erő a hátrahúzóval együtt egy ideig növekszik, majd a felfelé ható erő rohamos csökkenése következik. A lapjával szélben tartott tenyéren már csak hátrahúzó erő ébred (2.2. ábra).

Foglaljuk össze a tapasztalatokat! Ha a tenyéren ébredő R légerővektorokat egy pontból felmérjük, és a vektorok végpontjait összekötjük, akkor egy adott áramlási sebességhez tartozó, a testre jellemző görbét, ún. polárist kapunk. Minden R vektort fel szokás bontani egy áramlásra merőleges és egy áramlásra irányuló YX összetevőre; az előzőt felhajtóerőnek, az utóbbit pedig ellenállásnak nevezik.

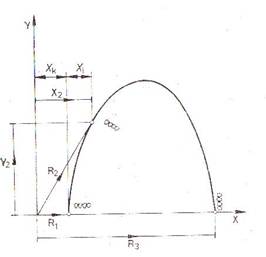
2.2. ábra.

Emberi tenyér polárisa

Az ellenállás nagy része az áramlásba tartott test mögött keletkező örvények következménye (2.3. ábra). A szélben élével tartott tenyéren ellenállást elsősorban a tenyér felületén súrlódó elakadó levegőrészecskék keltenek. Lapjával a szélbe fordított tenyéren a tenyér előtt torlódó részecskék nyomást, mögötte pedig szívást létesítenek. Az áramlásra szögben tartott tenyér a részecskéket erővel eltéríti, sebességük irányát megváltoztatja. A légerő az eltérítéshez szükséges erő reakcióereje: a részecskék a tenyeret felül szívják, alul pedig nyomják. Az ellenállás nagysága az eltérítés mértékétől függ. Minél meredekebb szögben éri az áramlás a testet, annál nagyobb az áramlás irányába eső összetevő, az ellenállás.

Az áramlásba helyezett test felületének egyenetlenségeiből, érdességéből a súrlódási ellenállás, a nyomáskülönbségekből pedig az alaki ellenállás származik. Az alaki ellenállásnak a részecskék eltérítéséből eredő része az indukált ellenállás ami tehát együtt jár a felhajtóerővel. Minden egyéb ellenállás, amely csak az X összetevőt növeli, repülési szempontok miatt károsnak minősül. A 2.2. ábra szerint R₁ légerő tehát lényegében súrlódási, az R₂ pedig alaki ellenállás. Egyikből sem származik az áramlásra merőleges erő, ezért mindkét esetben káros ellenállásról van szó. Az R₂ légerő X₂ összetevője tartalmazza a káros, elsősorban a súrlódási ellenállást és a nyomáskülönbségekből származó alaki ellenállást.

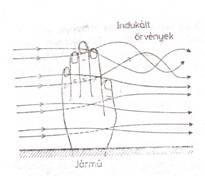
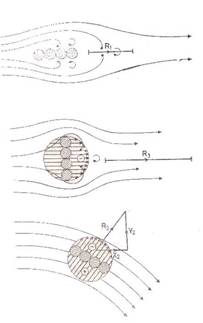
2.3. ábra.

Örvénylések a tenyér körül

Mivel ez a nyomáskülönbség felhajtóerőt is létrehoz, ezért az így keletkező alaki ellenállás egyúttal indukált ellenállás is.

Felhajtóerő keltésére való testeken, szárnyakon a felhajtóerő és az ellenállás az

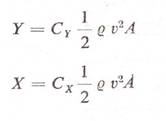
képletekből számítható, ahol q a levegő sűrűsége, v a megfúvás sebessége, A pedig a szárny alaprajzi területe. A C_y felhajtóerő- és a C_x ellenállás-tényező csupán a test geometriai viszonyaitól függ. Két test közül az az alkalmasabb szárnynak, amelyiken azonos alapterület, áramlási sebesség és közegsűrűség mellett a felhajtóerő és az ellenállás aránya, azaz a C_y/C_x hányados nagyobb. Az összetartozó C_x és C_y értékeket diagramban ábrázolva a szárny úgynevezett Lilienthal-féle polárisa adódik.

A jó arányt hajlékony szárnyakon a sajátos szerkezeti kialakítás teremti meg. A levegőt függőlegesen a szárnynak a gerinctartóval párhuzamos, függőleges síkokkal kimetszett szelvényei, a vitorla profiljai térítik el (2.4. ábra). Ha a vitorla alakját két körkúppal közelítjük, akkor a vitorlaprofilok közelítőleg hiperbolák. Merevszárnyak széles profiljaival összevetve, a vitorlaprofil a széles profil középvonalára emlékeztet. A vitorlaprofil húrja a profil két végpontját összekötő egyenes szakasz, állásszöge a húr és a megfúvás iránya által bezárt α szög, íveltsége pedig az m/h hányados.

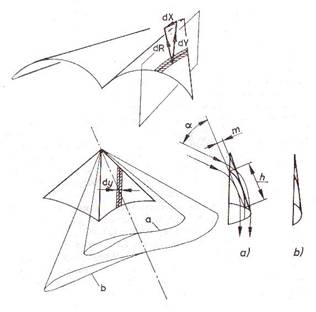
2.4.ábra.

Hajlékony szárny profiljai

a)öblös; b)feszes vitorlán

A szárnyon keletkező R légerő a profil mentén húzódó elemi dy szélességű sávon ébredő elemi dR légerők összege. A sáv szélességének kijelölése és az összegzés elvégzése felsőmatematikai feladat, azonban gyakorlatilag megfelelő közelítő képet kapunk, ha a sávot igen keskenynek képzeljük és az eredő légerőt a nagyszámú sávon ébredő dR erők összegeként kezeljük. Az elemi légerő éppen úgy felbontható ellenállásra és felhajtóerőre, mint egy teljes szárny esetében. Az elemi ellenállás és elemi felhajtóerő számítására a

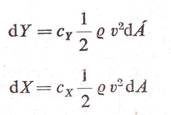
képletek alkalmasak. Itt

az elemi légerő tehát arányos a profil húrhosszával, c_y és c_x pedig a profilra vonatkozó tényezők A profil ellenállás- és felhajtóerő-tényezőjét a vitorlaprofilokra vonatkoztatott Lilienthal-féle polárisból lehetne leolvasni. Vitorlaprofilok polárisának kimérésével Eiffel foglalkozott, az ő eredményeit foglalja össze a 2.5 ábra (1. még a [15]-ben). Eiffel kísérleteihez ívelt, alaktartó lemezeket használt, ezért eredményeit csak becslésekre lehet felhasználni. A profilok íveltsége, a legnagyobb íveltség helye ugyanis kismértékben ugyan, de függ a megfúvás irányától és erősségétől is.

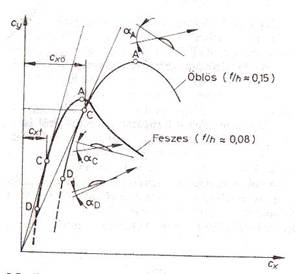
2.5.ábra.

Vitorlaprofilok Lillienthal-féle polárisa

A diagramokból a vitorlaprofilok néhány jellegzetességére következtethetünk. A D ponthoz tartozó α_D állásszögnél kisebb állásszöggel repülve a profil elveszti kúpszelet alakját, és lobogni kezd. A lobogó vitorlán keletkező légerő a szárny vázától, a vitorla merevítésétől és a lobogásgátló segédberendezésektől függ. A belobogás a normál repülési helyzetekhez tartozó állásszögek alsó határát jelöli ki. A diagram C pontjaihoz tartozik a legnagyobb felhajtóerő-ellenállás arány. Feszesebb vitorlán ez az arány egy bizonyos minimális íveltségig növekedhet, az íveltség további csökkenésével azonban az arány romlik. Az A ponthoz tartozó α_A állásszög esetén termelődik a legnagyobb felhajtóerő. Mivel feszesebb vitorlának kisebb a felhajtóerő-tényezője, ezért ugyanakkora felhajtóerő létrehozásához a feszesebb vitorlájú szárny nagyobb megfúvási sebességet igényel. Az állásszöget α_A fölé növelve, az áramlás már nem követi a profilt, hanem arról leválik; a profil átesik. A leválás az ellenállás növekedésével és a felhajtóerő csökkenésével jár. Feszes vitorlán a felhajtóerő csökkenése rohamosan megy végbe; kis állásszög-növekedésre is nagy felhajtóerő-csökkenés következik. Ugyanez a folyamat öblös vitorlán lassabban, átmenettel jelentkezik. Az átesési helyzet a normál repülési helyzetekhez tartozó állásszögek felső határa.

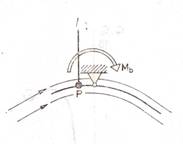
2.6.ábra.

A nyomásközépponton kívül megtámasztott profilt a légerő M_b

Bólintónyomatékkal forgatja

A profilon keletkező felhajtóerő az ún. nyomásközéppontban támad. (2.6. ábra.) Ha a profil merev lenne, akkor ebben a P pontban megtámasztva megfúváskor nem billenne egyik irányban sem: a profil egyensúlyban lenne. A P pont helyzete azonban függ az állásszögtől: az állásszög növekedésével a légerő előre, csökkentésével pedig hátra vándorol. Az egyensúlyi helyzetből kismértékben elfordítva, a profil automatikusan továbbfordul; magától nem tér vissza az egyensúlyi helyzetbe. A vitorlaprofil egyensúlyi helyzete tehát labilis.

Az elemi légerőket összegezve elvileg a teljes vitorlán ébredő légerő is meghatározható. A szárny állásszögén általában a szárnytartók síkja és az áramlás által bezárt szöget értik. A vitorlán ébredő R_v légerőt a pilóta testén, a sodronyokon és a vázon ébredő ellenállás módosítja. Mivel ezek az elemek felhajtóerőt nem keltenek, ezért ellenállásuk teljes egészében károsnak minősül. (2.7. ábra.) Gyakorlatilag egy szárny Lilienthal-féle polárisát tesztelőkocsin végzett mérésekből lehet meghatározni. Egy ilyen mérés eredményeit tünteti fel a 2.8. ábra. A szárnyat erőmérő műszerek kapcsolják az autóhoz; a légerő nagysága és hatásvonala a műszerekről egyidejűleg leolvasott értékekből adódik A 2.8. ábra a felhajtóerő- és az ellenállás-tényezőkön kívül a kereszttengely körül mért bólintónyomaték C_M tényezőjét is feltünteti A légerő nyomatéka a C_M tényezővel felírva:

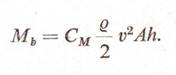
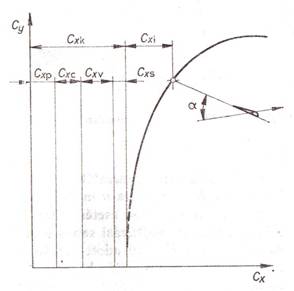
2.7. ábra.

C_xi az indukált ellenállás-tényezője; C_xk a káros ellenállás tényezője; C_xc a váz ellenállás tényezője;

C_xv a vitorla ellenállás tényezője; C_xs a sodronyok ellenállás tényezője; C_xp a pilóta ellenállás tényezője

A három tényező ismeretében merevszárnyakon a légerő minden adata kiszámítható tetszőleges v megfúvási sebességek esetén. Hajlékony szárnyakon adott állásszög esetén, különböző megfúvási sebességek hatására a légerő nem a megfúvási sebesség négyzetével arányos, ezért a 2.8. ábra görbéi is csak egy adott megfúvási sebességre érvényesek. Az optimálisnál nagyobb terhelés hatására ugyanis a vitorla és a váz deformálódik, ezért a felhajtóerő tényezőjének csökkenésére és az ellenállástényező növekedésére lehet számítani. Ez gyakorlatilag annyit jelent, hogy nagyobb terhelés hatására a szárny teljesítménye romlik, kis terhelés esetén viszont a szárny stabilitása válhat kérdésessé.

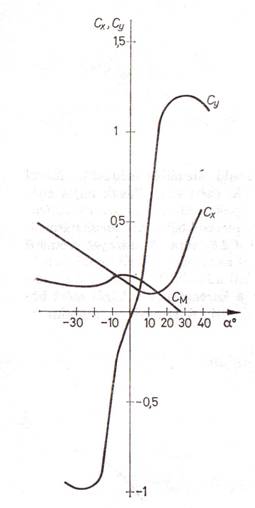
2.8. ábra.

Egy sárkány teszteléséből származó jellemző görbéi a [24] alapján

_{♣ Archiválta SRY 2005. január 18. ♣ CANON LiDE system ♣ Microsoft Word ♣ SRY MODELL 2005}