---

---

Eredeti megjelent:

Műszaki Könyvkiadó

Budapest 1980

43. old … 52. old.

Dr. Ordódy Márton

Sárkányrepülés (II.)

I.	2. Mint a madár 2.1. A siklószárny mozgásai 2.2. A felhajtóerő keletkezése
II.	2.3. A siklás
III.	2.4. A forduló 2.5. Különleges repülési helyzetek 2.5.1. Átesésre visszavezethető repülési helyzetek
IV.	2.5.2. A vitorla átlobbanására visszavezethető repülési helyzetek
V.	2.6. Siklószárnyak teljesítménye

2.3.

A siklás

A szárny egyenes vonalú, állandó sebességű mozgását siklásnak nevezzük. Nyugvó levegőben a v siklósebesség a függőleges irányú W vízszintes u utazósebesség vektori összege (2.9. ábra). A η siklószög csak kivételes esetekben csökken 20° alá; így az utazósebesség nagyságára nézve jól megközelíti a siklósebesség nagyságát. Az eredő légerő a sebességekből alkotott vektorháromszöghöz hasonló módon bontható ellenállásra és felhajtóerőre. Az ε siklószám tehát egyaránt meghatározható az utazó- és a merülősebesség, ill. a felhajtóerő és az ellenállás hányadosából (mi, a szakirodalomtól eltérően a közkeletű szóhasználat szerint értelmezzük a siklószámot) :

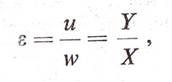
vagy a légerők számítására való képleteket felhasználva

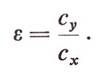
A szokásos siklóhelyzetekben a felhajtóerő nagysága az eredő R légerő nagyságát jól megközelíti.

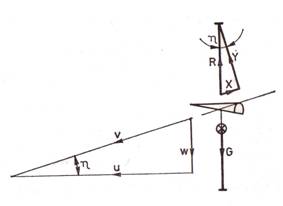
2.9. ábra.

A siklás sebesség és erőviszonyai

A lehetséges állandósult siklósebességeket egy pontból felmérve és a sebességvektorok végpontjait összekötve a siklószerkezet teljesítményét jellemző sebességi poláris adódik (2.10. ábra). Az A ponthoz tartozó ún. átesési sebesség a szerkezettel repülhető legkisebb sebesség. Ennél kisebb sebességgel a szárny tartósan siklani nem tud. Ha a pilóta mégis erre kényszeríti, akkor a szárny előrebukik és automatikusan gyorsulni kezd, átesik. A B ponthoz tartozó sebesség a legkisebb merülősebesség. A kezdőpontból húzott érintő a legnagyobb siklószámot eredményező v_C sebességet jelöli ki. A siklószárny maximális sebességének általában szilárdsági szempontok szabnak határt: a szárnyat a D pont fölé gyorsítva veszélyes rezgésekre, a váz törésére vagy a repülési tulajdonságok rohamos változására kell számítani. Egyes sárkányokat (pl. Héja) a pilóta nem is képes egy meghatározott v_D sebesség fölé gyorsítani. A sebességi poláris minden levegőnél nehezebb repülőszerkezetet jellemez; a 2.11. ábra a motor nélküli szerkezetek polárisait tünteti fel.

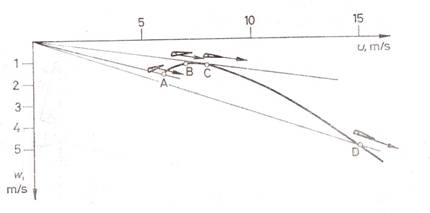
2.10.ábra.

Második nemzedékbeli sárkány sebességi polárisa.

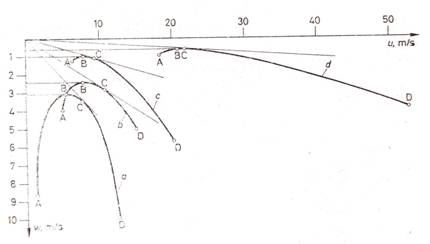
2.1. ábra.

Siklószerkezetek sebességi polárisa

a siklóernyő; b első nemzedékbeli sárkány; c harmadik nemzedékbeli sárkány ; d vitorlázó repülőgép

A különböző siklósebességekhez eltérő súlyponthelyzetek tartoznak. Ahhoz, hogy a szárny tartósan v_A sebességgel haladjon, a pilótának testsúlyát hátra kell helyeznie. A siklás azonban csak akkor lehet állandó sebességű, ha a légerő és a súlyerő egyensúlyának feltételei megvannak, azaz a légerőnek is hátra kell vándorolnia. A 2.12. ábra a légerő hossztengely menti vándorlását szemlélteti. Az ábrából látszik, hogy a pilóta testhelyzete és a szárny állásszöge között egyértelmű összefüggés van. Szokás a pilóta testhelyzetét a felfüggesztés és a trapéz síkja által bezárt szöggel jellemezni. Az összetartozó állás- és testeltolási szögeket diagramba lehet foglalni, és így a szárnyra jellemző testeltolás-diagramot kapjuk (2.13. ábra).

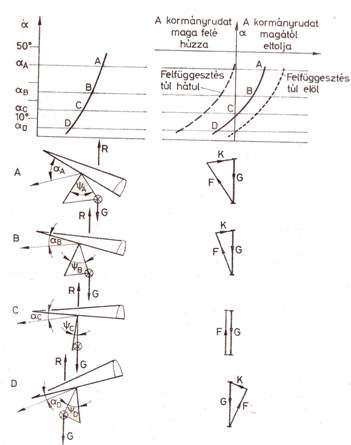
2.12. ábra

A légerő vándorlása a hossztengely mentén és a kormányerő megszerkesztése

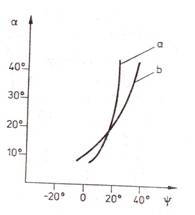
2.13. ábra

Testeltolás diagramok

A kevésbé stabil; b erősen stabil sárkány diagramja

A kormányerők nagysága szintén jellemzi a siklószerkezetet. A pilóta karjára jutó erő a pilótára ható erők egyensúlyából szerkeszthető meg. A 2.12. ábrán a folyamatos vonal egy olyan szárny állásszög-kormányerő diagramja, amelyen az optimális siklószöghöz tartozó sebességgel repülve a pilótának nem kell erőt kifejtenie, akár el is engedheti a kormányrudat. Ha ennél gyorsabban kíván repülni, akkor a kormányrudat folyamatosan húznia, ha lassabban, akkor folyamatosan tolnia kell. Ha a felfüggesztés túlságosan előrekerül, akkor a kormányerők a pontozott görbe szerint változnak: megnő tehát a tolóerőigény. Ha a pilóta a kormányrudat elengedi, akkor a D ponthoz tartozó nagy sebességű siklás állandósul. Hátrakerült felfüggesztés esetén a kormányrudat állandóan húzni kell; a kormányrúd elengedésekor pedig a sárkány orra fokozatosan emelkedik, végül pedig a pilóta beavatkozása nélkül átesik.

A siklás közben előforduló és különböző állásszögekhez tartozó egyensúlyi i siklóhelyzeteknek stabilaknak kell lenniök. A stabilitás vizsgálatához először tételezzük fel olyan zavarást, amely kizárólag állásszögváltozást idéz elő. Ha a szárny állásszöge változatlan pilótahelyzet esetén, megváltozik, és a szárny magától igyekszik az előző állásszög felvételére, akkor a kereszttengely körüli stabilitás vagy más néven a hosszstabilitás feltétele teljesül.

A hossz-stabilitás létrejötte a 2.14. ábra szerinti modell tulajdonságaiból vezethető le. Képzeljünk el két egymás mögött elhelyezkedő és egymáshoz mereven rögzített súlytalan szárnyat. Tegyük fel, hogy a szárnyak állásszögét változtatva az egyes szárnyakon ébredő légerők mindig azonos pontban támadnak, azaz a modell szárnyprofiljain a légerővándorlás elhanyagolható. A szárnyak alá képzeletben rögzítsünk mereven G súlyú anyagi pontot. A modell legfontosabb sajátossága az, hogy a. hátsó szárny állásszöge kisebb. Az ábra bal oldalán a szárnyakra jellemző állásszög-felhajtóerő-tényező diagramokból az eredő légerők nagyságára lehet következtetni. Az a) esetben az első szárnyon kétszer akkora felhajtóerő - és így közelítőleg kétszer akkora légerő - ébred, mint a hátsó szárnyon. A két erő eredője a két részerő között mért távolság első harmadában metszi a modellt. Ha a súly az eredő hatásvonalára esik, akkor megfelelő megfúvási sebesség esetén az egyensúly létrejöhet.

Billentsük ki a modellt Δα szöggel! A két szárny felhajtóerő-tényezője most csak kismértékben különbözik egymástól; az eredő is közel esik a részerők között mért távolság feléhez. Jelen esetben a hátsó szárny nagyobb részt vállal az eredő légerő létrehozásában, tehát az eredő hátravándorol. A légerő hátrahelyeződésének mértékét növelni lehet egyrészt a két szárny közötti távolság, másrészt a két szárny állásszöge közötti különbség növelésével. Mivel most a súlypont nem illeszkedik az eredő hatásvonalára, ezért a modellt az előző állásszög felvételére kényszerítő

nagyságú visszatérítő bólíntónyomaték keletkezik, ahol k a légerő karja. A súlypont és az eredő légerő hatásvonalának távolodása csak részben köszönhető a légerő k₂ mértékű hátravándorlásának. A modell elfordításakor a sülypont előrehelyeződése a k₁ távolsággal növeli a súlypont és a légerő távolságát. Az utóbbi jelenség a modell ingastabilitása. A modell előrebuktatásakor az első szárnyon növekszik a légerő, az eredő légerő pedig a nagyobb részerőt létrehozó elülső szárny felé vándorol.

A stabil légerővándorlás megteremtéséhez többfajta elrendezés terjedt el. Repülőgépeken a hátsó szárny szerepét a vízszintes vezérsík játssza; ebben az esetben a vezérsík állásszöge a főszárny állásszögénél kisebb. Kacsa-elrendezésű repülőgépeken a vízszintes vezérsík a főszárny előtt helyezkedik el, ezért állásszöge a főszárny állásszögénél nagyobb. Csupaszárny-repülőgépeken a szárny hátranyilazása révén a szárny közepe előrébb, a szárnyvégek pedig hátrébb kerültek. A szárny elcsavarásával gondoskodni lehet arról, hogy a hátrébb levő szárnyvég profiljai kisebb állásszöggel repüljenek. Előrenyilazott szárny éppen ellenkező elcsavarás esetén válik stabillá, azaz ha a szárnyvég állásszöge a nagyobb.

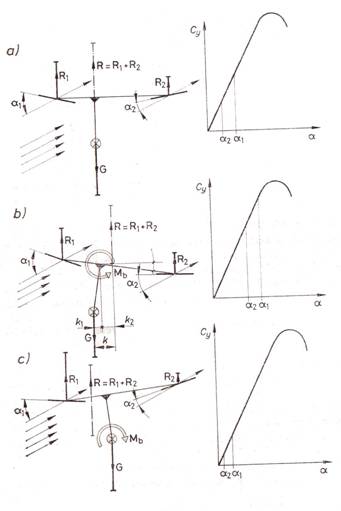
2.14.ábra.

Siklószárny hossz-stabilitásának létrejötte.

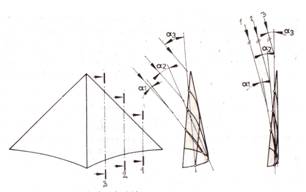
2.15. ábra

Sárkányok profilelrendeződése.

A sárkányok orrszöge általában 140^°-nál kisebb, a hátranyilazást így a váz határozza meg; a szárnyelcsavarás pedig a vitorla öblössége révén jön létre. A 2.15. ábra körkúp alakúnak feltételezett vitorla profilelrendeződését szemlélteti. Öblösebb vitorlának nagyobb, feszesebbnek kisebb az elcsavarása. Stabilitási problémák akkor keletkeznek, ha a vitorla belobban, és így az elcsavarás csökken vagy esetleg meg is szűnik. A stabil felhajtóerő-vándorlás feltételét a 2.12 és 2.13. ábrából lehet leolvasni. Az állásszög visszaállítására törekszik, azaz hossz-stabil a szárny, ha a felhajtóerő-vándorlás- és a testeltolódás-diagramok balra lejtenek. A pilóta a hossz-stabilitást a kormányerők közvetítésével érzékeli: a kormányerőknek az állásszöggel arányosnak kell lenniök.

Minél nagyobb a felhajtóerő-vándorlás mértéke, annál stabilabb a szárny. Két sárkány közül tehát az a stabilabb, amelyiknek a felhajtóerő-vándorlás- és a testeltolás-görbéje a 2.12. és 2:13. ábrák koordinátarendszerében kevésbé meredek. Két szárnyból álló modell esetében a stabilitást növelni lehet a két szárny távolságának növelésével. Vitorlaszárnyon ugyanezt a hatást a különböző állásszögű profilok hossz menti eltolásával, vagyis a hátranyilazás növelésével lehet elérni. Növeli a stabilitást, ha a modell szárnyai közötti állásszögkülönbség növekszik. Csupaszárnyszerkezeten a hossz mentén eltolt profilok közötti állásszögkülönbséget az elcsavarás hozza létre. A sárkányok hossz-stabilitását tehát alapvetően a nyilazás és a vitorla öblössége határozza meg. Vitorlaszárnyakon a profilok húrhossza a repülőgépeken mérhető húrhosszakhoz képest nagy, így - ellentétben a modell szárnyprofiljaira tett feltevéssel - a vitorlaprofilon létrejövő labilis légerövándorlás is jelentősebb. Ennek legyőzésére indokolt tehát erős nyilazást és határozott elcsavarást alkalmazni.

Feltételezhető olyan zavarás is, amely a szárny függőleges tengely körüli elfordulását okozza. Ilyenkor a szárny - tehetetlensége révén - egy ideig még az eredeti irányban halad tovább. Az így keletkező oldalazó mozgás a csúszás. Ha a csúszás hatására olyan legyezőnyomaték keletkezik, amely a csúszást megszüntetni igyekszik, akkor a szárny iránystabil. Hátranyilazott szárnyon a szél felé forduló félszárnynak nagyobb az ellenállása, így a szerkezetet az eredeti siklási irány felé forgató M_l legyezőnyomaték ébred (2.16. ábra). Az iránystabilitás növelését a repülőgépeken megszokott vezérsíkokkal is növelni lehet, amelyek akár a gerinctartó végén, akár pedig a szárnyvégen is elhelyezkedhetnek (1. Super Scorpion, Phoenix 10).

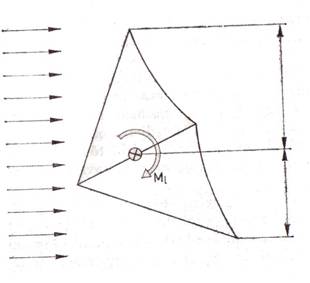
2.16.

Szélzászló stabilitás.

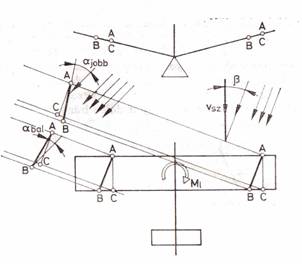
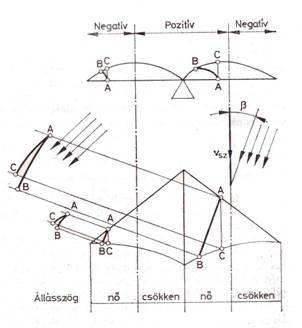
2.17.

Siklószárny V-állása

A csúszás megszüntetésében a nyilazáson kívül az un. V-be állítás játszik szerepet. A 2.17. ábrán síklapokból összeállított szárny V-be állítása látható. Ha a hossztengely irányú megfúvás helyett β szög alatt éri az áramlás a szárnyat, akkor az egyes eredeti AC hosszúságú α állásszögű profilok helyett AB hosszúságú szárnymetszetek keletkeznek, amelyek állásszöge a megfúvás felőli félszárnyon növekszik, az ellenkező oldalon pedig csökken. Az állásszög megváltozásának következtében az ábra szerinti jobb szárnyon nagyobb, a bal szárnyon kisebb indukált ellenállás keletkezik, amely a szárnyat az áramlás irányába fordítani, azaz a csúszást megszüntetni igyekszik. Lefelé irányított, azaz negatív V-állású szárnyon ellentétes irányú legyezőnyomaték ébred, ezért az ilyen szárny önmagában, nyilazás nélkül irány-instabil.

Szerkesszük meg egy vitorlaszárny ferde metszeteit! A szárny középső részén, a szél felőli félszárny profiljainak állásszöge nő, az ellentétes oldalon pedig csökken. A szárnyvégeken éppen az ellenkezője történik. A vitorlaszárny közepe tehát úgy viselkedik, mintha pozitív, a szárnyvégek pedig mintha negatív V-állásúak lennének. A szárny középső, nagyobb húrhosszú része a felhajtóerő és így az indukált ellenállás létrehozásában nagyobb részt vállal, ezért az olyan sárkányon, amelyen a szárnytartók és a gerinctartó egy síkban vannak, a középső rész stabilizáló hatása érvényesül. Nem szükségszerű azonban, hogy a három tartó egy síkba essen. Csökken a V-állás, ha a vitorlát a taréj segítségével a gerinc fölé emeljük. Új típus optimális V-állását pedig a kereszttartó végeihez futó sodronyok hosszának változtatásával lehet beállítani.

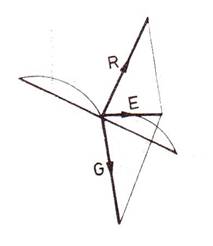
2.18. ábra.

A siklószárny csúszása

Ha a zavarás a szárny megdőlését okozza, akkor a lég- és a súlyerő eredője oldalirányú gyorsulást hoz létre. Ha a megdőlés nem párosul elfordulással akkor a szárny a dőlés irányában megcsúszik (2.18. ábra).

Pozitív V-állás esetén a megfuvás felőli félszárnyon a profilok állásszöge következtében több felhajtóerő keletkezik, ezért a szárny törekszik az eredeti vízszintes helyzet felvételére. Az iránystabilitás vizsgálatakor azonban megállapítottuk, hogy a csúszás révén a csúszás irányába fordító legyezőnyomaték is ébred, ezért a megdőlést előidéző zavarás egyúttal elfordulást is okoz. Az orsózó és a legyező mozgás kapcsolódásában a vitorla deformációja is szerepet játszik, amire a fordulóba vitel kérdésénél fogunk részletesebben kitérni.

_{♣ Archiválta SRY 2005. január 18. ♣ CANON LiDE system ♣ Microsoft Word ♣ SRY MODELL 2005}