![]()
II.
A levegő hatása a mozgásban lévő
testekre.
Öreg földünket, ezt a folyton forgó sártekét, mintegy 320 km magasságig levegő veszi körül. Ez a mindnyájunkat részéről ismeretes nitrogén és oxigénvegyület – a maga baktériumhalmazával, porával, vízgőzével és gázával – nemcsak a földnek tengelye körül való forgásban vesz részt, hanem sűrűségének folytonos változása miatt is örökös forrongásban, mozgásban van. Ma szélcsend uralkodik, holnap már viharok tombolnak s a feltornyosult hullámhegyek ismét völgybe gördülve, síkokká lapulnak a végtelen levegőtengerben.
Repülőgépeinkre tehát nagy feladatok várnak, amikor meg kell küzdeniök ezekkel a láthatatlan áramlatokkal. A bátor pilótát nem menti meg bátorsága, ha tapasztalatlanul, a levegő hatásainak ismerete nélkül száll fel a magasba; modellrepülőgépünket is csak a pusztulás érheti, ha ezen elveknek alkalmazása nélkül bocsátjuk első útjára. A modellkészítőnek tehát épúgy, mint a pilótának, tisztában kell lennie mindazokkal a hatásokkal, melyeket a levegő a mozgásban lévő testekre kifejt.
Tapasztalati tény, hogy a levegő –bármily gördülékeny kis részecskékből van is összetéve- a benne mozgó testekkel szemben bizonyos nagyságú ellenállást fejt ki, amelyet légellenállásnak nevezünk. Ez az ellenállás megnehezíti, sőt, ha túlságosan nagy meg is akadályozhatja a testnek mozgását.
Ha egy síklemezt először élével, másodszor meg lapjával mozgatunk a levegőben előre, az utóbbin erősebben érezzük a levegő nyomását, mint az előbbin. S ez természetes is, mert a levegő az első esetben csak a lemez éléhez ütközhetett, míg a másodikban a lemeznek egész felületéhez. A levegő ellenállása, nyomása tehát arányos a benne mozgó felületnek nagyságával. Minél gyorsabban mozgatjuk lemezünket, annál erősebb ellenállást érzünk. A megfigyelések és számítások hosszú sora szerint ez az ellenállás a sebesség négyzetével arányos, ami azt jelenti, hogy ugyanazon körülmények között a kétszer olyan sebességgel mozgó lemez négyszer, a háromszor olyan gyorsan mozgó pedig kilencszer nagyobb ellenállást érzünk.
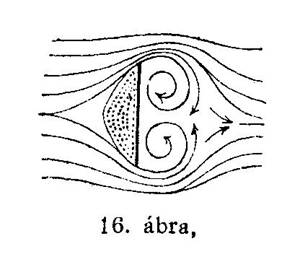
Amikor a lemezt élével mozgatjuk előre, akkor a levegőrészecskék az élnek ütődve, párhuzamosan, simán, szinte hatástalanul siklanak el a lemez két oldalán. Egészen más jelenséget észlelünk a második esetben, amikor lemezünket lapjával, vagyis függőleges állásban mozgatjuk előre. Mint a mellékelt 16-ik ábránkon látjuk, a levegő ilyenkor a lemez mellső oldalának a közepén kúposan összeszorul, majd e kúpról, mint a dara a kúposra öntött tányérról, lesiklik, hogy aztán a lemez mögött örvénylő mozgásokat végezhessen. A levegő tehát most erős nyomást fejt ki a lemez mellső oldalán, mögötte pedig légritka teret alakít, mely viszont hatalmas szívóhatást gyakorol a lemez hátsó felületére.
Világosan láthatjuk ebből, hogy a mozgás irányára merőlegesen álló felületeket a repülőgépeknél nem szabad alkalmaznunk. Szépen csökkenthetjük a levegő ellenállását, ha a lemez elé egy féltojásalakú toldalékot, mögéje pedig egy hosszan elnyúló, úgynevezett lefolyó felületet illesztünk (17. ábra). Ezen ugyanis a legkisebb ellenállással, örvénylés nélkül siklanak tovább a levegőrészecskék.
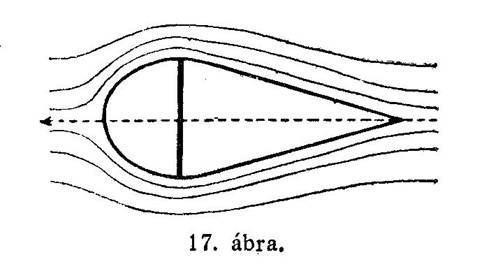
A mozgást gátló erő pedig az így kidolgozott testeknél, melyeket áramvonalalakú testeknek szoktunk nevezni, jóformán csak a gyenge surlódásból keletkezik. S e formára a természet tanított meg bennünket, amikor a madarak és a halak példáját, vagy az ereszről lehulló vízcseppeknek a képét idézte emlékezetünkbe. A vízcsepp ugyanis gömbalakban hagyja el az ereszt, gyorsuló esése közben mindjobban megnyúlik, míg végre áramvonalalakúvá válik (18. ábra). Ezért hívjuk az áramvonalalakot cseppalaknak is. A levegő tehát a könnyen idomítható anyagból olyan alakot formál, melynek légellenállása a legkisebb.

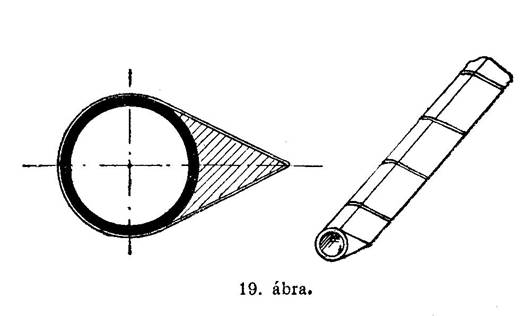
A repülőgépek megépítésénél nagy gondot kell fordítanunk a levegő ellenállásának a csökkentésére. Elsősorban a törzset kell áramvonalalakúvá kiképeznünk s abban minden lehető alkatrészt elrejtenünk, burkolnunk. Ilyen alakot kell adnunk a futószerkezet támasztó csöveinek s a szárnytartó rudaknak is. A csövek mögé a 19-ik ábrán látható módon fatoldalékot, lefolyó felületet iktatunk, melyet meghatározott térközökben vékony dróttal erősítünk a csövekhez.
Általában megjegyezhetjük, hogy sokkal rosszabb egy négyzetes testet csak elöl hegyes, vagy tompa orral ellátni, mint elöl változatlanul hagyva, hátul lefolyó felülettel kiegészíteni. Bár annak a követelménynek, hogy a repülőgépen minden áramvonalalakú legyen, nem felelhetünk meg, mégis törekednünk kell erre minden olyan részen, ahol csak kivihetjük.
Növeli a levegő ellenállását a repülőgép alkotórészeinek a levegővel való surlódása is. Ennek csökkentésére tehát a gépnek a levegővel érintkező minden egyes részét a lehető legsimábbra kell kidolgoznunk s azután lakkal vagy politúrral bevonnunk.
Ügyelnünk kell még a drótoknak fellő kifeszítésére is. A laza, lengő drótok ellenállása csaknem másfélszer akkora, mint a jól kikötött, feszes állású drótoké.
Amikor lemezünket vízszintes helyzetben mozgattuk előre, akkor az alatta elvonuló levegőnek minden egyes része legalább egy pillanatig a lemez alatt marad, itt megszorul s mint ilyen gyenge kis nyomást fejt ki a felette lévő lemezre, amellyel ezt mintegy alátámasztotta. A következő pillanatban már kisurran a lemez alól, hogy újabb részecskének adhassa át helyt. Ha most a lemezünkkel egyenlő területű, de hosszabb felületet választunk s ezt mozgatjuk ugyancsak vízszintes helyzetben, hosszabbik élével előre a levegőben, akkor azt tapasztaljuk, hogy az alátámasztó erő most jóval nagyobb, mint az előbbi esetben. S ez természetes is, mert a keskenyebb, hosszúkás felületek két oldalán jóval kevesebb levegő illanhat el, mint a szélesebb, rövidebb felületformáknál. Látjuk tehát, hogy az alátámasztó vagy emelő erő arányos a felület hosszával. Ezért adott a természet hosszúkás szárnyat a madarak ezreinek; ezért igyekszünk mi is a madarak példáját követve gépmadarainknál is ezt az elvet megvalósítani.
A repülőgépnél rendkívül fontos szerepe van ennek az alátámasztó vagy emelő erőnek. A kutatások hosszú sora indult meg az irányban, hogy ezt az erőt, amelytől tulajdonképpen gépünk felszállása függ, minél jobban érvényesíthessük, kihasználhassuk. S vizsgálódásaink nem maradtak eredmény nélkül. Sok sok kísérlet és próba után végre is rájöttünk mindazokra a tényezőkre, melyektől ezen emelőerőnek a nagysága legelsősorban függ, s melyeknek kiaknázása ép ezért a repülőgépeknek úgyszólván életkérdése. Főképpen a felületeknek megfelelő szögbeállítása, helyes ívelése és lekerekítése játszanak itt szerepet, melyekhez még a felületek vastagságának helyes megválasztása s a legjobb sárnyformának a felhasználása járul.
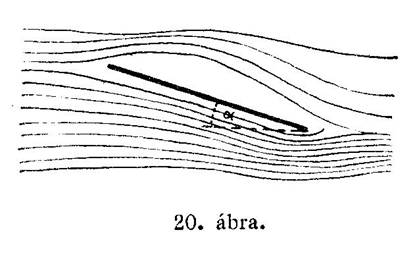
Ha az eddigi kísérleteinkhez használt lemezünket ferde helyzetben, vagyis a vízszintessel szögbeállítva (α) mozgatjuk a levegőben előre, akkor a lemez aljához tóduló levegő 20-ik ábrán látható módon a lemez alatt összeszorul és felfelé nyomó hatást fejt ki; míg a lemez felső részén légritka tér képződik s a már ismeretes szívóhatást hozza létre.
Ez az alulról nyomó s felülről szívó erő egyszerre hat, amit a lemez mozgatásakor, mint ellenálló és emelő erőt rögtön meg is érzünk. Ha ezeket az alulról nyomó s felülről szívó erőket, melyek a lemez felületének pontjaiban merőlegesen hatnak, az erők parallelogrammájának tétele alapján összegezzük, akkor a keletkező eredőerő ugyanazt a hatást fejti ki, mint a lemezre ható tényleges erők együtt véve. Azt a pontot, amelyben ez az eredő erő a felületet támadja, nyomásközéppontnak, magát az eredőerőt pedig az annyiszor emlegetett légi erőnek mondjuk. Mellékelt 21-ok ábránkon a légerőt R-rel, nyomásközéppontot pedig T-vel jelöljük.
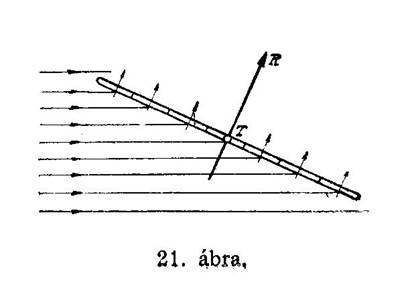
A légi erő, mint már említettük, egyrészt visszaszorító, másrészt emelő hatást fejt ki. Ép ezért két egymásra merőleges alkotóra bonthatjuk: a vízszintes irányú Rx visszahajtó erőre, mely a mozgó lemezt mozgásában gátolja s az Ry felhajtó erőre, mely a lemezt tulajdonképpen a magasba emeli (22. ábra).
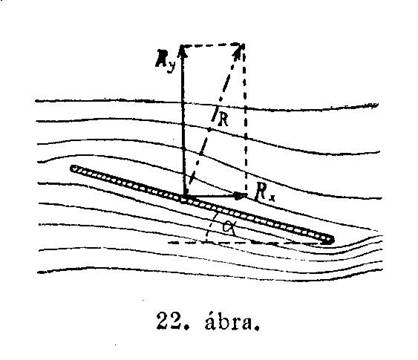
Íme a repülőgépek repülésének, felemelkedésének a miértje. Ha ugyanis a felhajtó erő legyőzi a teljesen felszerelt gépnek súlyerejét, akkor a gép a magasba száll s a légcsavarnak forgása közben szabadon repül előre.
A kísérletek tanusága szerint, a megfelelően görbített felületek sokkal hatásosabbak a síkfelületeknél. A görbefelületek mellett ugyanis a levegőrészecskék nyugodtabban áramlanak el, minek következtében azután egyrészt kisebb az ellenállásuk, másrészt meg nagyobb a felhajtó-erejük. Hogy ez miként lehetséges, azt a 23-ik ábránk alapján világosan megérthetjük. Ezen ábránkon szárnyfelület-keresztmetszetek, vagyis szárnyprofilokat látunk. Ha ilyen profilokat mozgatunk a levegőben előre, akkor a levegőrészecskék nem úgy haladnak el a profil előtt, mint ahogyan ezt a legfelsőn láthatjuk, hanem mivel a levegő a felület alatt képződő légritka teret a legmohóbban igyekszik betölteni, a középső profilon feltüntetett módon. A levegő tehát felfelé irányuló mozgást is végez A szárnyfelület alatt keletkező légritkulás természetesen a távolabb eső részecskékre is kihat, azokat is felfelé szívja, hogy így még nagyobb erőt fejthessen ki a felület alsó részére. Ezen szívó hatás miatt nevezzük a felületnek aa vonalig terjedő részét szívórésznek. Ez a szívóhatás kiterjed a felület előtt lévő levegőrészecskékre is, úgyhogy a levegő már jóval a felület előtt kezdi meg lefelé irányuló mozgását. Ez az oka annak, hogy a felület fölé kerülő levegőrészek nem ütköznek a profil kiemelkedő részébe, hanem szépen elsiklanak a szívórés fölött anélkül, hogy az emelőerőkkel ellentétes irányú, leszorító hatást fejtenének ki.
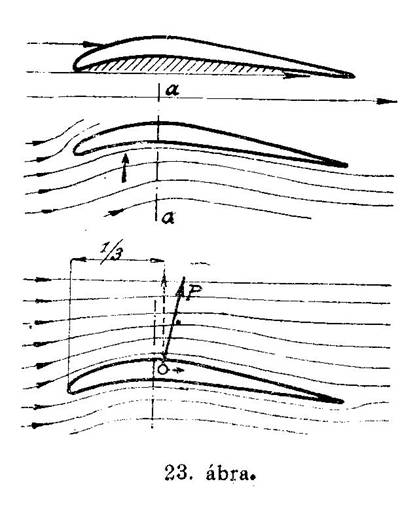
A szívórész mögött az aa vonal után pedig, a szívórész előtti irányukat megtartva, ritkulást idéznek elő, amint ezt a legalsó profilon szemléltetjük. A felület fölött létesített ezen újabb szívóhatás a felületet csak újból emeli, még pedig csaknem kétszer oly erővel, mint az alsó, mert az összes emelő erőnek mintegy kétharmad részét teszi.
Még nagyobb lesz az emelő erő, ha ezeket a profilozott felületeket a vízszintes síkkal szögbeállítjuk. A felhajtó erő ugyanis a beállítási szög növekedésével általában növekszik. Ez a növekedés azonban 0°-tól csak körülbelül 15°-os beállítási szögig tart, míg ennél nagyobb szögek esetén a felhajtóerő csökken s a felület függőleges helyzeténél, vagyis 90°-os beállításnál zérus lesz. A visszahajtóerő ellenben mindig annál nagyobb, mennél nagyobb a beállítási szög. A beállítási szöget ezért úgy választjuk meg, hogy a felhajtóerő meglehetősen nagy, a visszahajtóerő pedig lehetőleg kicsiny legyen.
A tapasztalatok szerint legjobb 3-6°-os beállítási szöggel dolgozni. Sohase állítsunk felületet 15°-os szögbe. Bizonyos esetekbe, mint például az igen nagy görbületű és vastag profiloknál, a 0° is sokszor megfelel.
A beállítási szög változását rendesen nyomon követi a nyomásközéppontnak a vándorlása is. Ez a pont a síkfelületeknél 0°-os beállítás esetén a mellső vagy belépő élen, 90°-os beállításesetén pedig a felület mélységének a közepén van. Görbefelületeknél pontos helyét csakis laboratóriumi kísérletekkel tudjuk meghatározni. A felületnek leginkább használni szokott 2-6°-os beállításnál rendesen a szárnyfelület mélységének első harmadában fekszik, amint ezt a 23-ik ábránkon szemléltettük is. A beállítási szög növelésekor előbbre, annak csökkentésekor hátrább húzódik. A nyomás középpont helyzetének az ismerete, amint ezt még hallani fogjuk, főképpen a szárnyfelületeknek a gépen való pontos elhelyzése a s vele kapcsolatos stabilitási szempontokból fontos.
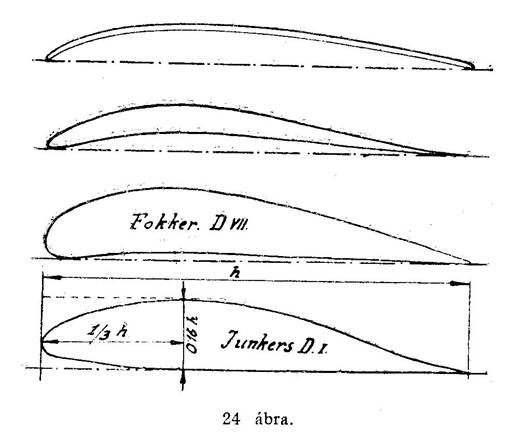
A felhajtóerő nagyságát még a felületek vastagsága is befolyásolja. Az újabb kísérletek igazolása szerint ugyanis a vastagprofilú felületeken, amilyent például a 24-ik ábránk 3. és 4. esete ábrázol, kicsiny visszahajtó erő mellett, meglehetősen nagy felhajtóerő keletkezik. A 3-ik a Fokker, a 4-ik a Junkers-profil. Legkedvezőbb ez ilyen profil akkor, ha első harmadában a legvastagabb. Ez a vastagság a profil két végpontját összekötő húrnak, vagyis a profil h mélységének 0,16 része legyen. Az ilyen profilt alul nem is görbítjük, hanem, mint ezt a Junkers profilnál látjuk, egyenes vonallal határoljuk.
A felhajtóerőre nézve igen fontos még az is, hogy a felületek felett és alatt elsurranó levegő lehetőleg a szárny támadó élére merőlegesen vezessük tova. A levegő ugyanis a felület mozgásakor egyrészt ennek oldalán, másrészt meg mögötte a lehető leggyorsabban igyekszik kiszökni, úgyhogy ennek meggátolására a szárnyformák megépítésénél feltétlenül gondolnunk kell.
Nem helyeselhetjük tehát a legegyszerűbb szárnyfelületeknek, a négyszögletes szárnyformának az alkalmazását, mert ezeknek az oldalán a levegőrészek áramlása a fellépő szívó és nyomó hatások következtében rossz. Mint a mellékelt 25-ik ábránkon látjuk, az ilyen szárnyfelületeknek a végén, a vonalkázva megjelölt háromszögből a levegőrészek kitódulnak s a szárnyak fölött levő légritka térbe hatolva a felhajtóerőnek hatását megzavarják s az ellenállást is növelik.
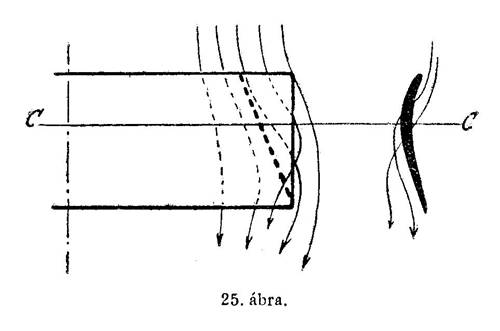
Éppen ezért a zárnyaknak ezen káros hatású részét rendesen levágjuk. Így alakul ki a Morane-Saulnier-gépeken használatos szárnyforma.
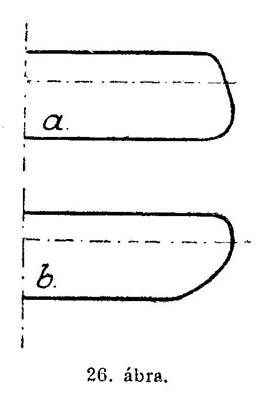
Még jobb a hatás, ha a háromszög levágásakor keletkezett sarkokat a 26-ik ábrának a mintája szerint legömbölyítjük.
A levegőnek a szárny végeken való kiszökését még úgy is korlátozhatjuk, hogy a szárnyaknak végét hátul kissé mélyebbre kerekítjük le, mint elől. Az így készült szárnyaknál ugyanis a szárnyak belső, szélesebb részén átvonuló levegőrészecskék nagyobb súrlódásnak vannak kitéve, mint a keskenyebb szárnyvégeknél átáramlók, aminek következtében az előbbieknek sebessége jóval kisebb, mint az utóbbiaké. A szárnyvégeken nagyobb sebességgel átáramló levegő tehát mintegy határt, korlátot von a kiszökni készülő levegőrészek elé. A levegő ilymódon a szárnyvégeken alig tér el eredeti irányától. Mellékelt 26-ik ábránkon a b. eset szemlélteti ezt a szárnyformát, mely különben Blériottól ered.
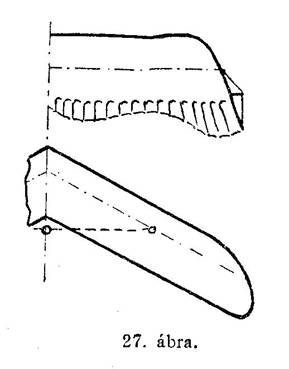
A régi osztrák repülőknek igen kedvelt formája az Etrich galamb szárnyforma, amelynek képét a 27-ik ábránk felső mintáján mutatjuk de. Ugyanezen ábrának az alsó része egy nyílrepülőnek visszahajló szárnyát szemlélteti. Ezekről a nyílrepülőkről később még hallani fogunk.
Amint a szárnyak oldalán, úgy azok mögött is meg kell akadályoznunk az alátóduló levegőnek hirtelen kisiklását. A különböző kísérletek eredményeképpen arra a tapasztalatra jutottunk, hogy ezen követelménynek a legegyszerűbben úgy felelhetünk meg, hogy a szárnyak alá szoruló levegőnek fogvatartására a felületek hátsó részét a szárnykereten túl, könnyen lengő szegély formában meghosszabbítjuk.
Rendkívül fontos még a szárnyak szélességének, mélységének a viszonya a szárnyak hosszúságához. Hallottuk már, hogy az egyenlő területű felületek közül a hosszabbik felületen nagyobb a felhajtó erő, mint a szélesebben. A felületek hosszának és szélességének a megválasztásánál tehát bizonyos arányt kell betartanunk. A kísérletek szerint legjobbak azok a felületek, amelyeknek mélysége a hosszúságnak 6-od és 8-ad része között váltakozik, vagy más szóval, amelyeknél a szárnyfelületek mélysége úgy aránylik azok hosszához, vagyis a gép terjedtségéhez, mint az 1:6-hoz, illetőleg 1:8-hoz.
♣ Archiválta SRY 2007 június 25. ♣ CANON
LiDE system ♣ Microsoft Word ♣ SRY MODELL 2007