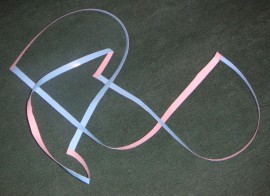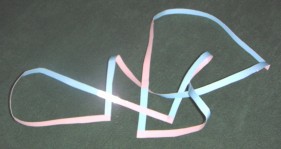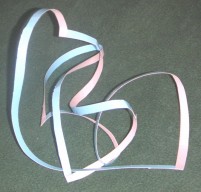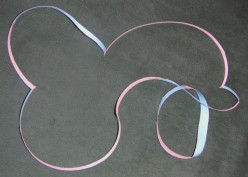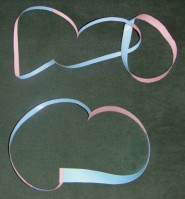6. KERESZTBEN ÖSSZERAGASZTOTT SZALAGOK
Két szalagot össze lehet ragasztani úgy, hogy széleik egymásra merőlegesen találkozzanak, keresztben. Itt a felületek egymáshoz való rögzítése miatt új tulajdonságok jelennek meg, ami merőben eltérő struktúrát fog eredményezni topológiailag. Gondolunk például arra, hogy az oldalak gyakorlatilag egymásba olvadnak. A ragasztás területét ugyanis úgy kell tekintenünk, mintha a két felület eggyé válna. Ekkor egy elágazó felületet kapunk, ami rugalmas nyújtással is előállítható lokálisan.
6.1. KÉT JOBBOS CSAVARODÁSÚ SZALAG
6.1.1. SZIMMETRIKUS FELHASÍTÁS
Két Nullás-szalag: keresztben összeragasztva továbbra is kétoldalúak maradnak, holott külön kétszer kétoldalúak voltak. Mindkettőt felvágva egy síkban kiteríthető, négyzet formájú és kétoldalú sávot kapunk.
Nullás és Szimplás-szalag: együtt egyoldalú felülettel rendelkeznek. Kétféleképpen is felvágható, attól függően, melyik felhasításával kezdjük, mégis ugyanazon struktúrához jutunk. Egy sík négyzethez, kétoldalú sávhoz, ami viszont a felületi jellemzőit tekintve különbözni fog az előzőtől, lásd később. Ha csak a Szimplásat vágjuk fel (k2j0j1s1bt), a felület megmarad egyoldalúnak, ha a Nullásat, kétoldalúvá válik (k2j0j1s1at).
Nullás és Duplás-szalag: együtt kétoldalúak. Bármelyiket vágjuk fel először, marad kétoldalúnak és ugyanolyan sík négyzetet kapunk, mint a két Nullás-szalag esetében.
Nullás és Triplás-szalag: együtt egyoldalúak. Ugyanazon szabály érvényes rá, mint a Nullás és Szimplás-szalagra.
Nullás és Tetrás-szalag: együtt kétoldalúak, mint a Nullás és Duplás esetében.
Nullás és Pentás-szalag: együtt egyoldalúak, mint a Nullás és Szimplás esetében.
Összefoglalva: ha egy Nullás-szalagot keresztben összeragasztunk egy bármilyen csavarodású egyszerű szalaggal, felhasítva őket mindig sík négyzetet kapunk. De attól függően, hogy a másik szalag csavarodási száma páros (k2paros) vagy páratlan (k2paratlan), a négyzetsáv felülete kétféle lesz.
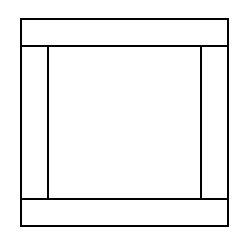
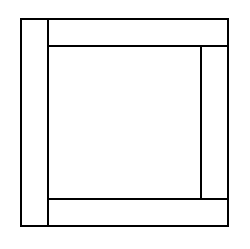
Két Szimplás-szalag: együtt egyoldalúak. Ha csak az egyiket vágjuk fel, marad egyoldalúnak, ha viszont mindkettőt, a rendszer a szalagok világában teljesen egyedülálló módon szétesik két különálló szalagra (k2j1j1s2t). Mindkettő kétoldalú lesz, a csavarodási fokokat lentebb összefoglaltuk egy táblázatban.
Szimplás és Duplás-szalag: együtt egyoldalúak.
Szimplás és Triplás-szalag: együtt egyoldalúak.
Szimplás és Tetrás-szalag: együtt egyoldalúak.
Szimplás és Pentás-szalag: együtt egyoldalúak.
Két Duplás-szalag: együtt kétoldalúak.
Duplás és Triplás-szalag: együtt egyoldalúak.
Duplás és Tetrás-szalag: együtt kétoldalúak.
Duplás és Pentás-szalag: együtt egyoldalúak.
Két Triplás-szalag: együtt egyoldalúak.
Triplás és Tetrás-szalag: együtt egyoldalúak.
Triplás és Pentás-szalag: együtt egyoldalúak.
Két Tetrás-szalag: együtt kétoldalúak.
Tetrás és Pentás-szalag: együtt egyoldalúak.
Két Pentás-szalag: együtt egyoldalúak.
Összefoglalva: egyoldalú szalag egy és
kétoldalúval keresztben összeragasztva egyoldalú rendszert
alkot. Kétoldalú szalagok összeragasztva megmaradnak kétoldalú
rendszernek. Két egyoldalú szalag összeragasztva és felhasítva
az első lépésben mindig két szalagot alkot, amik a két
Szimplás-szalag speciális esetét kivéve össze lesznek fonva.
Az alábbi táblázatban összefoglaltuk a fenti
szalagok felhasításakor kapott szalagok csavarodási értékeit.
Vagyis, hogy milyen csavarodású szalagot milyennel
összeragasztva és ezt szimmetrikusan felhasítva, az első
lépésben mekkora csavarodású szalagokat kapunk. Amint látható, a
mátrix átlósan tükörszimmetrikusnak mutatkozik.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6.1.2. ASZIMMETRIKUS FELHASÍTÁS
A keresztben összeragasztott szalagok aszimmetrikus felhasítását nem minden variációra végeztük el, csak az "izgalmasabbakra". Az eddigiekből nyilvánvaló, hogy a kétoldalú szalagok aszimmetrikus felhasítása nem eredményez új struktúrát, ezért őket kihagytuk az alábbi sorozatból.:
Nullás és Szimplás-szalag: sík négyzet lesz belőle, rajta egy Möbius-szalaggal.
Nullás és Triplás-szalag: sík négyzet lesz belőle, rajta egy Triplás-szalaggal.
Két Szimplás-szalag: két részre szétesik, plusz a 4x180-os csavarodást tartalmazó szalagon egy Möbiusszal.
Szimplás és Triplás-szalag: mint az előző. Itt is a nagyobb csavarodási számú szalagon lesz egy Möbius.