A modellrepülés elmélete (2)

<< előző rész  |  következő rész >>

A repülés alapelvei

A felhajtóerő keletkezése.

A légerő

A természet alkotta legkisebb ellenállású test az esőcsepp alakja. Ez az alakja a “szimmetrikus” szárnyszelvényeknek, az áramvonalas test mögött alig keletkeznek örvények. Alaktényezője a legkedvezőbb, de ha a cseppalak középvonala párhuzamos a körülötte kialakult áramlás irányával, csak F_x irányú - dinamikai - ellenállás keletkezik, felhajtóerő (F_y irányú) nem.

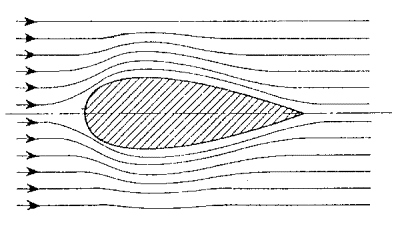
A csappalak mögött alig keletkeznek örvények

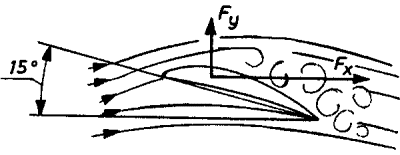
Ha egy síklapot ferde helyzetben tartunk - vagy mozgatunk - az áramlás irányában, a síklapra ható erő két összetevőre bontható.

A függőleges (y irányú, F_y) és a vízszintes (x irányú, F_x) erőkre. Az F_y a dinamikai felhajtóerő, vagy emelőerő, az F_x a dinamikai ellenállás erője. E két összetevő aránya a lapnak a mozgás irányával bezárt szögétől és a lap alakjától függ. Síklap esetén az ellenállás sokkal nagyobb, mint az emelő erő.

A légerő keletkezése

A csepp alakú keresztmetszetet - a szimmetrikus szárnyszelvényt - céljaink szerint aszimmetrikussá kell tenni. Ez esetben a szárny közvetlen közelében nyomásváltozások keletkeznek. A szárnyszelvény felett az áramlás sebessége nagyobb lesz, tehát a nyomása csökken, míg alatta a sebesség lecsökken, tehát a nyomása növekszik. Ezt fokozni lehet azzal hogy a szelvény orrpontját - a torlópontot - és a végpontot összekötő egyenest - ez a szelvény húrja - az áramlás irányára valamilyen szögbe állítjuk.

Felhajtóerő keletkezése aszimmetrikus szárnyszelvényen

A szelvényen már 0 fokos szög mellett is keletkezik felhajtóerő, de ezt a húr néhány fokos szögbe állításával még növelni lehet. Ezt a szöget nevezzük “állásszögnek” (a )

Ilyen asszimetrikus szárnyszelvénynél az ellenálláshoz viszonyítva jelentős felhajtóerőt lehet elérni. A keletkező felhajtóerő egyenesen arányos a közeg sűrűségével és a szárny felületével.A felhajtóerő nagyságát gyakorlati úton levezetett képlettel lehet kiszámítani:

Ahol
F = a felhajtóerő N-ban,
r = a levegő sűrűsége: 1,25 kg/m³
v = az áramlás sebessége m/s-ban
A = szárnyfelület m²-ben
c_f = mértékegység nélküli arányossági tényező, a “felhajtóerő-tényező”

Egy szárnyforma gyakorlati mérésénél a felhajtóerő, az áramlás sebessége mérhető, a levegő sűrűsége és a szárnyfelület adott, tehát csak egy ismeretlen maradt, a felhajtóerő-tényező (c_f)

A képletből megállapítható a felhajtóerő-tényező szerepe: a torlónyomást és a szárnyfelületet ezzel szorozva kapjuk meg a felhajtóerőt.

A felhajtóerő - adott szárny esetén - a legnagyobb mértékben az állásszögtől függ.

Példa:

F1A -(A/2) modellen keletkező felhajtóerő:

F = a felhajtóerő N-ban,
r = a levegő sűrűsége: 1,25 kg/m³
v = az áramlás sebessége m/s-ban: = 4 m/s
A = szárnyfelület m²-ben: = 30 dm² = 0,3 m²
c_f = mértékegység nélküli arányossági tényező, a “felhajtóerő-tényező” (példánkban legyen = 1 )

behelyettesítve a fenti értékeket:

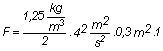
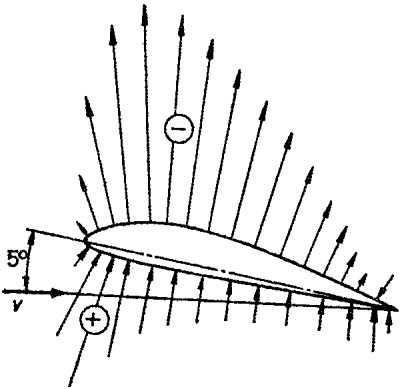
A felhajtóerő eloszlása a szárnyfelületen

A szárnyfelületen keletkező légerő - felhajtóerő - iránya és nagysága sok tényezőtől függ, (ezek közül az egyik legfontosabb az állásszög) .de a fő összefüggések itt is állandóak. A legfontosabb a nyomás eloszlása a szárny körül. A szárny felett áramló közegnél (levegőnél) az áramlás gyorsul, tehát a nyomása csökken. Az alsó részén az áramlás lassul, a nyomása növekszik. E két változás a szárnyszelvény mentén minden pontban mérhető. Ezek a mérések azt bizonyították, hogy a “felhajtóerő” 1/3 része tulajdonítható a szárnyfelület alatti, a 2/3 része a szárnyfelület feletti nyomásváltozásnak.

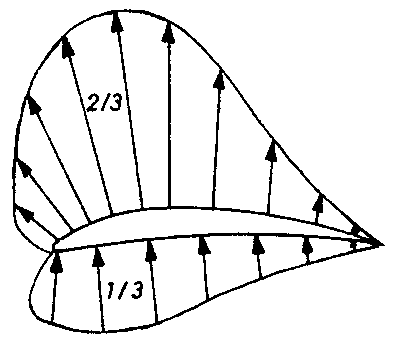
A nyomásváltozás eloszlása a szárnyszelvény hossza mentén.

Ezek az erők is változnak a szárnyszelvény hossza mentén. Az erők - ha pontonként vizsgáljuk azok nagyságát, azt tapasztalhatjuk, hogy - általában - a szelvény legvastagabb pontja felé közeledve egyre nagyobbak, e pont mögött csökkennek. A sok-sok erő által elfoglalt terület arányos a szárny által keltett felhajtóerővel.

Az állásszög

Az állásszög a szárnyszelvény belépőélét (torlópontját) a kilépőéllel összekötő egyenes (a szárnyszelvény húrja) és az áramlás irányával bezárt szög. Mérése vastagabb szelvényeknél körülményesebb, vékony ívelt szelvényeknél könnyebb.

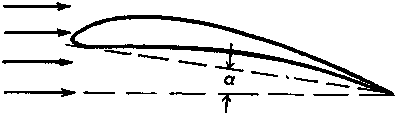
Az állásszög.

Az állásszög mérése

Az állásszög elméleti mértéke a szárnyszelvény húrja és az áramlás irányával bezárt szög. De ezt a földön kell tudni mérni, az áramlás irányát nekünk kell előre feltételezni és meghatározni.

Az állásszöget a tervrajzok különböző módon adják meg. Rendszerint valamilyen, a törzsön végigfutó egyenes léchez viszonyítják, esetleg a törzs felső, a középvonallal párhuzamos részén jelölik. Hiba, ha ugyanakkor a vízszintes vezérsík (csillapító) állásszögéről elfeledkeznek. Ekkor mindig feltételezhetjük hogy annak állásszöge a 0 fok, ezt természetesnek veszik és nem adják meg.

A szárny állásszöge
(A vízszintes vezérsík “állásszöge” 0 fok)

A gyakorlatban a “szárny állásszögét” - a vízszintes csillapító állásszögét “0 fok”-nak feltételezve - állítjuk be. (Az állásszögnek repülőmodelleknél - a szárnyszelvény alakjától függően - általában +1 és +5 fok között kell lennie. Ez vastagabb szelvényeknél a kisebb, vékonyabb, íveltebb szelvényeknél a nagyobb. )

Ezért - ha valaki külön beszél a szárny és külön a vízszintes csillapító állásszögéről, - az csak valami máshoz viszonyítva lehet érvényes. Például a törzs középvonalához, vagy a törzs felső síkjához viszonyítja mind a két szöget.

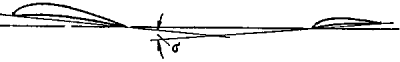
A szárny állásszöge
(A vízszintes vezérsík “állásszöge” negatív)

Példa:

A szárny “állásszöge” +3 fok,
a vízszintes vezérsík “állásszöge” -1 fok,
akkor a szárny valóságos állásszöge 3+1= 4 fok
(Ha a vízszintes csillapítónak is pozitív (+) állásszöge van, azt a szárnynál mért állásszögből le kell vonni !)

A mérés a legegyszerűbben végezhető el. A modell orrát enyhe szorítással satuba fogjuk, a törzs függőleges helyzetben legyen. A vízszintes vezérsík alá egyenes lécet (3x8, 5x10) fogunk pl. ruhaszárító csipesszel rögzítve. A lécnek fel kell feküdnie a vízszintes csillapító alsó felületén és le kell érnie a szárny alatt legalább a belépő élig.

Ezután megmérjük a léc távolságát a belépőnél, és a kilépőnél. A belépőnél mért távolságból kivonjuk a kilépőnél mért távolságot, ezt merőlegesen felmérjük egy egyenesre, amelynek hossza egyenlő a szárnymélységgel.

Az így kapott háromszög kisebbik hegyesszögét szögmérővel megmérjük.

Ez a szög a modell állásszöge.

(A mérésben pontatlanság van. A pontatlanság oka az hogy egyik esetben sem igazán a szárnyszelvény húrját tudtuk meghosszabbítani a léccel - sem a vízszintes csillapítónál, sem a szárnynál - de a napjainkban használatos vékony szelvényeknél az eltérés olyan kicsi, hogy sokat nem tévedtünk. A valóságban az állásszög az így mértnél valamivel nagyobb.)

Jelenségek az állásszög változtatásakor

Az állásszög változtatásával változnak a szárnyfelületen keletkező légerők:

a felhajtóerő, (F_y) és a
légellenállás (F_x).

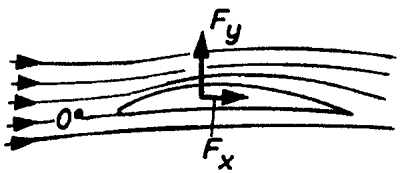
0 fokos állásszögnél az ellenállás a legkisebb

A modelleknél szokásos 4 - 5 fokos állásszögnél a felhajtóerő látványosan megnő, míg a légellenállás nem változott jelentősen.

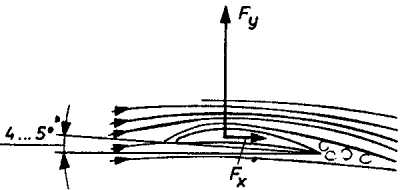
4-5 fokos állásszögnél a felhajtóerő nagyobb lett

Tovább növelve az állásszöget a felhajtóerő már számottevően nem növekszik, de elkezd növekedni a légellenállás.

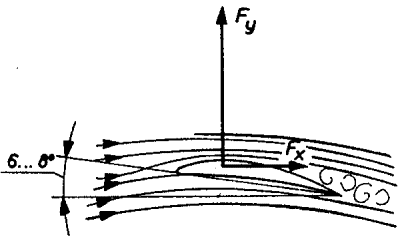
6-8 foknál már jelentősen növekszik a légellenállás

Minden szárnyszelvénynek van egy jellemző állásszöge amelynél az ellenállás hirtelen és nagyon megnő, ezzel együtt a felhajtóerő jelentősen lecsökken.

12-16 foknál hirtelen lecsökken a felhajtóerő és jelentősen megnövekszik a légellenállás

A jelenséget összefoglalva:

Az állásszög növelésével a felhajtóerő egy darabig nő, azután hirtelen nagyon lecsökken. Amíg kis állásszögeknél a felhajtóerő az állásszög növelésével egyenes arányban növekszik - a “görbe” vonala egyenes, - elér egy olyan állásszöget, amelynél már a szelvény felső oldalán a leválás kezd hamarabb bekövetkezni, ezután hirtelen nagyon megnő az ellenállás és nagyon lecsökken a felhajtóerő. Azt a pontot, amelyiknél az állásszög növelésével már nem nő tovább a felhajtóerő - hanem rohamosan csökkenni kezd,

kritikus állásszögnek

nevezzük.

Az összefüggéseket diagramban ábrázolva általános érvényű összefüggéseket kapunk. Ez az összefüggés minden szárnyszelvénynél eltérő mértékű, de a változások jellege, a fő törvényszerűség minden esetre igaz.

Ezt ábrázolja a következő diagram:

C_f felhajtóerő-tényező
a állásszög (fokban)

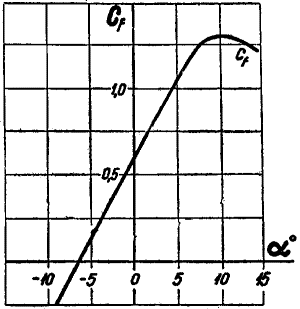
A “görbén” jól látható a felhajtóerő egyenletes növekedése az állásszög növelése esetén, ugyanilyen látványosan mutatja a felhajtóerő hirtelen csökkenését is ( a kritikus állásszög elérésekor.)

Mivel a felhajtóerő nagysága nagy mértékben függ a szárny állásszögétől, a felhajtóerő-tényező értéke az állásszög nagysága szerint változik. Ennek törvényszerűsége matematikai összefüggésekkel nem határozható meg, a kísérleti intézetek az általuk mért összefüggéseket diagramokban vagy táblázatokban adják meg - szárnyszelvényenként.

Ugyanilyen módon ábrázolhatjuk diagramban az ellenállás változásának összefüggéseit is.

Valamely test ellenállása a súrlódási és az alaki ellenállás összege

C_{e összes}= C_{e surl.} + C_{e alaki}

A test alakjától függő ellenállás-tényező: Az egységnyi keresztmetszeti felületű ( 1 m²) testnek egységnyi torlónyomás esetén C_e ellenállása van.

Bármely test kiszámítható ellenállása (C_összes) ezután:

C_ö = C_e . F _torló . A

Ahol C:_ö = a test összes ellenállása (N - ban)
C_e = a test ellenállás-tényezője mértékegység nélküli arányossági tényező
F: _torló = a torlónyomás (N/m² - ben)
A: = a test áramlás irányára merőleges felülete (homlokfelülete) (m²-ben)

Az ellenállás változása az állásszög függvényében - diagramban:

C_e ellenállás-tényező
a állásszög (fokban)

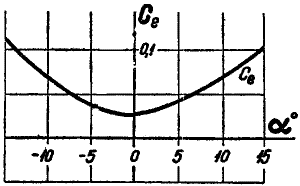
Az ellenállás változása is látható a diagramból. A legkisebb 0 fok környékén, előtte és utána mindig nagyobb.

A szárny ellenállása nagy mértékben függ a pontos kidolgozástól, a felület bevonásától is. A kísérletek során kapott értékek mindig a legpontosabban kidolgozott felületű szárnyakra vonatkoznak.

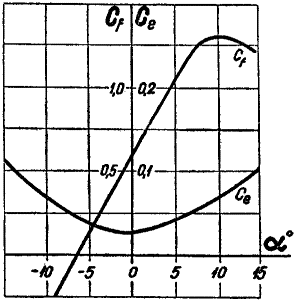
Ha a Cf felhajtóerő-tényezőt és a Ce ellenállás tényezőt egy diagramban ábrázoljuk, egyszerűen mérni lehet a legkedvezőbb állásszöget. Ahol a két vonal a legtávolabb van egymástól, azon a részen kell keresni a legkedvezőbb állásszöget.

(Azaz csak jó lenne ezt ilyen egyszerűen megmérni. Csak akkor lehetne, ha az adott szárnyra vonatkozó görbéket egy jól felszerelt szélcsatornában meg tudnánk mérni. Így csak a törvények közötti összefüggéseket ismerhetjük meg, de legalább ezek megismerése és felhasználása legyen mindenkinek természetes.)

Eddig vizsgáltuk az állásszög változásakor fellépő két legfontosabb mennyiség egymástól függő változásait - a felhajtóerőt és a légellenállást.

Az állásszög változásával együtt változik a felhajtóerők összegének - eredőjének - helye, azaz a támadáspontja is. Ezt a támadáspontot nevezzük a felhajtóerő

nyomásközéppontjának.

A nyomásközéppont

A nyomásközéppont a szárnyra ható összes (alul és felül jelentkező) erő összegének támadáspontja.

A nyomásközéppont az erők összegének támadáspontja.

Ez az erő-támadáspont általában a szárnyszelvény hosszának első harmadánál - 33%-nál - ébred. (Ez a szabály hagyományosan vastag szárnyszelvények és szimmetrikus csillapító szelvény esetén érvényes. A kivételekről és eltérésekről azok indokolásával együtt később lesz szó.)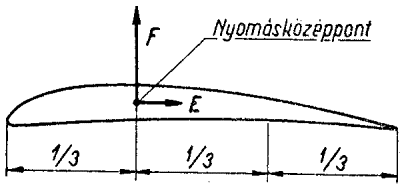

Az állásszög növelésével a nyomásközéppont a szelvény belépő- éle felé vándorol.

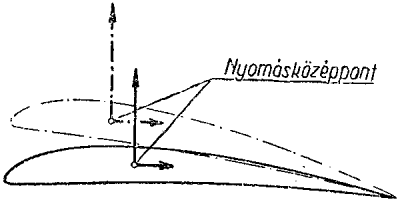
Nagyobb állásszögnél előrébb kerül a nyomásközéppont

Ez a változás annak tulajdonítható hogy nagyobb állásszögeknél a szelvény orrpontja - a torlópont - az orrgörbület mentén lejjebb helyeződik el, ezért az áramló levegőnek a szelvény alatt és a szelvény felett megtett útja - egymáshoz viszonyítva - megváltozik. A felül áramló levegőnek hosszabb utat kell megtenni, mint az alsónak

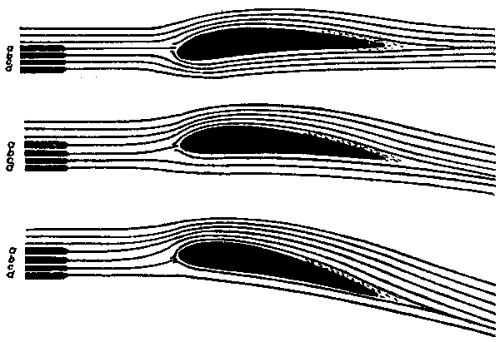
A következő ábra-soron ez jól látható.

Az első ábrán az “a”-val jelölt levegőáram ér a torlóponthoz, ez “válik kétfelé” és kerüli meg a szárnyszelvényt alulról-felülről. A torlópont a szárnyszelvény orrgörbületének felső részén keletkezik.

A második ábrán - 0 fokhoz közeli esetben - a “b” légárammal szemben alakul a torlópont, az orrgörbület “csúcsán” válik el az alsó és felső légáram.

A harmadik ábra jelentős állásszög mellett mutatja a légáramok útját. Itt a “c” áramlás vonala érkezik úgy az orrgörbülethez, hogy szétváljon alsó-felső áramlásra.

A nyomáseloszlásból származó légerő eredője nagyobb állásszögeknél a belépőhöz közeledik, állásszög csökkenés esetén távolodik - hátrább helyeződik.

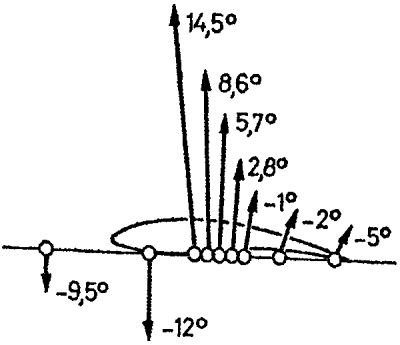
A nyomásközéppont helye - a szárnyszelvény első harmadában - csak hozzávetőleges érték. Pontos elhelyezkedését a kísérleti intézetek a szárnyszelvény adatai között adják meg, - a szárnymélység százalékában - mindig egy állásszöggel együtt. Ez az állásszög - és a hozzá tartozó nyomásközéppont helye - szorosan összefüggenek egymással. A nyomásközéppont az adott helyen csak ennél az állásszögnél van.

Az állásszög növelésével előbbre, csökkentésével hátrább kerül, de azt, hogy mennyivel, csak a mérést végző intézet tudná megmondani, vagy nagyon sok kísérlettel lehet közelítő pontossággal megállapítani.

Ezzel magyarázható az a közismert jelenség hogy állásszög növelése esetén a modell orrkönnyűvé, míg állásszög csökkentésnél orrnehézzé válik.

<< előző rész  |  következő rész >>