A modellrepülés elmélete (3)

<< előző rész  |  következő rész >>

A nyomatéki tényező

Ismétlés:
A nyomásközéppont szárnyszelvényenként más-más helyen van, az állásszög változásával változik a nyomásközéppont helye is.
Azt hogy egy szárnyszelvénynél hol számíthatunk a felhajtóerő eredőjének támadáspontjára, - a nyomásközéppont helyére - csak pontos mérésekkel lehet megállapítani. A nyomásközéppont helyét a szárnyszelvény hosszának százalékában adják meg, és a szelvény orrpontjára vonatkozik.

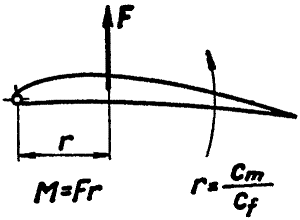
Ha az “F” felhajtóerő távolsága a szelvény orrától “r” távolságra ered, (nevezhetjük a felhajtóerő karjának is ) az erő és a távolság szorzata nyomatékot (M) eredményez:

ahol az F felhajtóerő Newtonban,
r távolságméterben
akkor az M nyomaték mértékegysége

Newton · méter

A fenti képletből a nyomaték karját kifejezve:

ahol r = a felhajtóerő karja - méterben,
q = torlónyomás N/m²-ben,
S = a szárnyfelület m²-ben,
t = a szárnyszelvény hossza m-ben
C_f = a felhajtóerő-tényező
C_m = a nyomatéki tényező

vagyis:

Ezek szerint a C_m/C_f hányados megadja a nyomásközéppont helyét a szelvény orrpontjától a szelvény hosszának százalékában.

 A kísérleti intézetek a szárnyszelvény mérésekor a felhajtóerő-tényező (C_f) és az ellenállás tényező (C_e) mellet meg szokták adni a szárnyszelvény

nyomatéki tényezőjét (C_m)

is, amely - mint minden tényező,- mértékegység nélküli szám. A nyomatéki tényező - ha más megjegyzést nem találunk mellette - a szárnyszelvény “orrpontjára” vonatkozik.

Előfordul hogy egyes kísérleti intézetek nem az orrpontra vonatkozó értéket adják meg, ezt (pl. a C _{m 0,25} ) a tényező mellé írt számmal jelölik. Ez a 0,25 azt jelenti hogy a nyomaték a szárnyszelvény - elölről számított - 25%-án átmenő tengelyre vonatkozik. Ez esetben a számításoknál ezt az eltérést figyelembe kell venni.

A nyomatékok ismeretében érthetjük meg hogy az általában a szárnyszelvény első harmadában ébredő nyomaték ellenére, miért lehet egyes modellek súlypontja a szárnymélység 50 - 55 %-ában.

Csak a szárnyon ébredő nyomatékkal számolunk, ha a vízszintes vezérsík szelvénye szimmetrikus. Ilyen csillapítószelvénnyel repülnek a körrepülő-műrepülő,(F2B) az RC műrepülő (F3A) a rádióirányítású modellek közül az F3B modellek. Ezeknél a súlypontot a szárnymélység első 1/3 részére kell tervezni.

 Ha a vízszintes csillapító is felhajtóerőt “termel”, azaz emelő csillapítót használunk, (szabadonrepülő modelleknél ma ez az általános) ennek felhajtóereje - bár kicsi - de az erő karjának jelentős hossza miatt jelentősen befolyásolja a két felhajtóerő összegének eredőjét

 A rajzon a súlypont és a szárnyon keletkező felhajtóerő = F_sz támadáspontjának távolsága = r_sz
A vízszintes csillapítón keletkező felhajtóerő = F_cs
támadáspontja és a súlypont közötti távolság = r_cs

Példa

Számítsuk ki egy A/2 (F1A) modell adatait az előző részben bemutatott C_f és C_e görbék adatai alapján.

Állásszögek:	csillapító:	0 fok Cf = 0,6
	szárny:	5 fok Cf = 1,1
Felületek:	szárny:	30 dm^2= 0,3 m^2
	csillapító:	4 dm^2 = 0,04 m^2
Sebesség:	v =	4 m/s
A levegő sűrűsége:	r =	1,25 kg/m^3

A felhajtóerő kiszámítása:

behelyettesítve a szárnyon keletkező felhajtóerő:

Kiszámítva:

A vízszintes csillapítón keletkező felhajtóerő

Kiszámítva:

(A csillapító távolsága a kilépő éltől legyen a szárnymélység (140 mm) négyszerese. Ha csak a szárnyat vizsgáljuk, a szárny felhajtóerejének támadáspontja a szárnymélység 30%-nál lenne. (Cm = 0,3 , ezt az adatot a szárnyszelvény koordinátáival és egyéb jellemző görbéivel együtt közli a mérést végző kísérleti intézet. Ez a 140 mm. 30%-a = 42 mm a szelvény orrpontja mögött.)

A csillapító szélessége 100 mm. Felhajtóerő támadáspontja 0 fokos állásszögnél a szélesség 33%-ánál van, ez a belépő mögött 33 mm-t jelent.

A modell súlypontja - az emelő csillapító miatt - a két felhajtóerő támadáspontja között kell lennie. Az előző ábrán jelölt távolságok és a hozzájuk tartozó felhajtóerők adják a súlypontra vonatkozó nyomatékot, amelyek egyenlők.

F_sz . r_sz = F_cs . r_cs

A két támadáspont közötti távolság:

r_sz + r_cs =

98 mm + 4.140 mm + 33 mm. = 691 mm = 0,691 m.

A távolságok a felhajtóerőkkel fordítottan arányosak.

F_sz : F_cs = r_cs : r_sz

Az összes felhajtóerő:

3,3N + 0,24N = 3,54N

A szárny felhajtóerő támadáspontja mögött

Ebből a súlypont szükséges helye

A szárnyon a felhajtóerő támadáspontja a szelvény orrpontja mögött 42 mm-el van, e mögött kell lennie a súlypontnak még 46,84 mm-el hátrább, összesen:

42 mm + 46,84 mm @ 42 mm + 47 mm @ 89 mm = 0,089 m

A súlypont helye a 140 mm-es szárnyszelvénynek a szárny orrpontjától számított 63,57%-nál van.

Próba: a számítások szerint
rsz = 46,84 mm,
rcs = 691 mm - 46,84 mm @ 644 mm

F_sz . r_sz = F_cs . r_cs

3,3 .0,04684 = 0,24 . 0,644

0,154572 = 0,15456

Eltérés - méterben számolva - csak az ötödik tizedes számjegyben van, tehát a számítás elfogadható.

Az indukált ellenállás

Ismétlés:(az 1. részből.)
A levegőben mozgó testekre ható ellenállások közül megismerkedtünk a

nyomási, vagy alaki ellenállással, ( C_{e alaki}) és

a súrlódásból ( C_{e surl}.) származó ellenállással

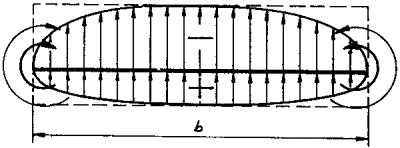
Ezek az ellenállások minden közegben mozgó testre vonatkoznak. A levegőben mozgó szárnyfelületen keletkezett - (alsó-felső) - nyomáskülönbség ki akar egyenlítődni. Ennek érdekében a szárny alsó és felső részén mozgó levegő iránya nem marad párhuzamos, hanem az alul áramló levegő áramlásának iránya eltér, és a szárny vége felé igyekszik, mert ott tud a leggyorsabban kiegyenlítődni.

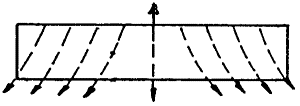
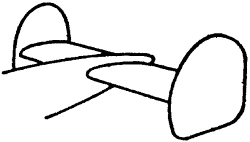
A szaggatott vonal a szárny alatt haladó levegő iránya
, a szárny felett haladó levegő a szárny (fesztávolság) közepe felé tér el,

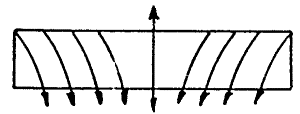
mert a szárny végén alulról felfelé örvénylő levegő a középvonal felé kényszeríti.

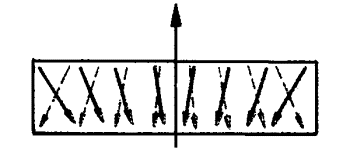
A szaggatott vonal az alsó, a folyamatos vonal a felső áramlás irányát jelzi.

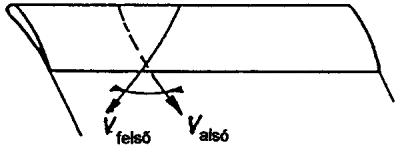
 Az áramló levegő - amint eléri a szárny végét, a nyomáskülönbséget kiegyenlítve feláramlik a szárnyfelület fölé.

A kilépőél mögött összetalálkozó áramlás nyomása már egyenlő, azonban a szárny felső és alsó oldala felől érkező levegőrészecskék sebességének iránya különböző. Az irány-különbség a szárnyfelület vége felé egyre nagyobb, a szárny szimmetriasíkja felé fokozatosan csökken.

Az áramlási irányok különbözősége miatt a szárny mögött örvények keletkeznek, az örvények a szárny vége felé húzódnak és két - a szárnyvégeken keletkező - örvénnyé alakulnak.

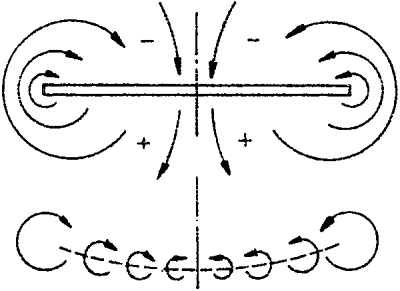
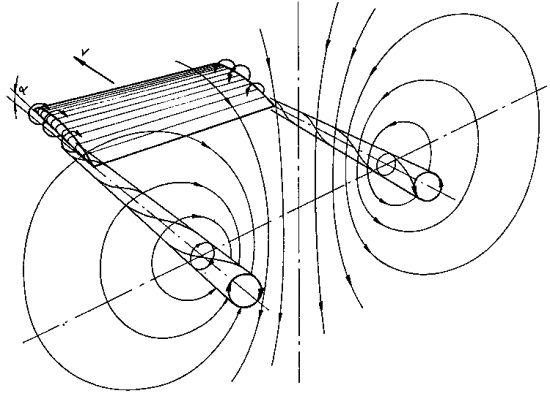
 Ha a szárnynak nem lenne “vége”, azaz végtelen nagy lenne a fesztávolság - nem jöhetne létre ez az örvényeket előidéző nyomás-kiegyenlítődés. Erre vonatkozó kísérletek eredménye volt a felületek végén alkalmazott, a repülési iránnyal párhuzamos síklap, - a “zárólap” - amely csak a vízszintes vezérsíkok végén terjedt el.

A gyakorlatban a szárny sohasem “végtelen” hosszú, ezért a szárny végén fellépő örvényeket okozó “feláramlással mindig számolni kell.

A szárnyfelület áramlási végén - a kilépőélnél - vizsgálva a levegő áramlásának irányát megállapították hogy ott a légáram iránya már nem vízszintes, hanem kissé lefelé irányuló. Úgy is mondhatjuk hogy a mozgó szárnyfelület a levegőt folyamatosan “lefelé mozgatja”

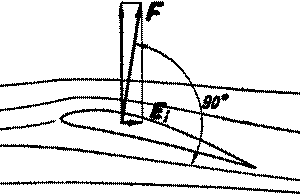
A hatás-ellenhatás elvének köszönhetően a lefelé mozgatott levegő által kapjuk a felhajtóerőt. A felhajtóerő az áramlás irányára merőleges. A szárnyszelvényen keletkező felhajtóerő a már lefelé eltérített levegő áramlásának irányára merőleges, ezért csak függőleges összetevője a gyakorlatban hasznos felhajtóerő, vízszintes összetevője - mint ellenállás jelentkezik. Ezt az ellenállást nevezzük

indukált ellenállásnak.

és a számításoknál E_ind - vagy röviden E_{i -} nek jelöljük.

A levegőáram irányváltoztatásának szögét nevezzük

indukált állásszögnek: a _i

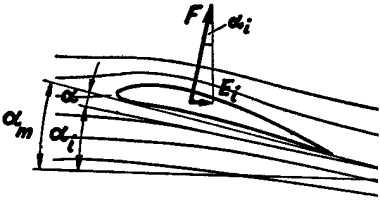
Így a valóságos repülési állásszög a beállított állásszöghöz viszonyítva ennyivel kisebb, vagyis

a _valóságos = a _geometriai - a _indukált

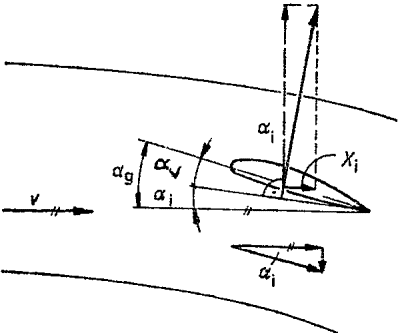
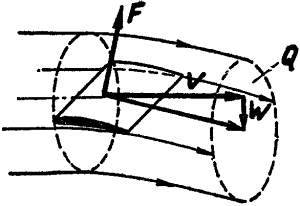
A szárny - repülés közben akkora levegőtömeget - levegőhengert - mozgat, mint a fesztávolságával megegyező kör átmérője

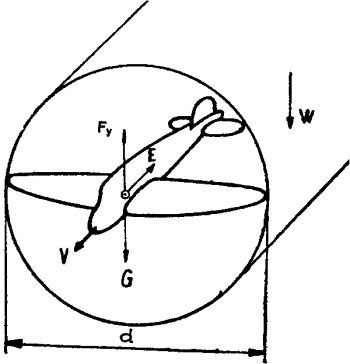
Mennyiségtanilag ezt úgy fogalmazhatjuk meg hogy a keletkező felhajtóerő arányos az időegység alatt megmozgatott levegő tömegével és arányos a lefelé történő elmozdulás sebességével.

Példa. (a három oldallal előrébb szereplő F1A modell adataival.)

ahol

F = a felhajtóerő N-ban, - 3 N
r = a levegő sűrűsége,.- 1,25 kg/m³
w = az áramlás függőleges sebessége - m/s-ban.
Q = a másodpercenként megmozgatott levegő térfogata, (a fesztávolsággal egyező átmérőjű henger térfoga ta)

Az első oldalon szereplő példában nem szerepelt a modell fesztávolsága (d), azért azt most adjuk meg: legyen d = 200 cm
= 2 méter

Először kiszámítjuk a léghenger keresztmetszetét: (A)

A megmozgatott léghenger térfogata (Q) = a keresztmetszet (A) és a vízszintes sebesség (v) szorzata:

Mi a vízszintes sebességet ismerjük. (v = 4 m/s) A függőleges sebesség (w) számítható a felhajtóerőből (mert ennek “ellenerője” a levegőeltérítésből származó felhajtóerő)

ebből

A levegő függőleges sebessége 0,191 m/s, ebből az eltérés szöge:

Az előző részben számított F1A modell esetében: 2 m-es fesztávolságnál akkor kapunk 30 dm² felületet ha a szárnymélység (a szárnyszelvény hossza) 15 cm.

Második példa, (egy sokkal karcsúbb szárny esetén):

Számítsuk ki az előző értékeket, de 250 cm-es fesztávval, 12 cm-es szárnymélységgel. Minden egyéb adat legyen azonos.

1. A léghenger keresztmetszete:

2. A másodpercenként megmozgatott levegőmennyiség:

3. A levegő függőleges sebessége:

4. Az eltérítés szöge:

A kisebb eltérítési szög azt jelenti hogy kisebb a levegőhenger eltérítése által okozott örvénylés, ezért

kisebb az indukált ellenállás is.

<< előző rész  |  következő rész >>