A modellrepülés elmélete (4)

<< előző rész  |  következő rész >>

Ismétlés:

A szárny alatti és a szárny feletti áramlás - a nyomáskülönbségek miatt - ki akar egyenlítődni. Ezt a kiegyenlítődést a legkönnyebben a szárnyak végénél éri el. Az alulról felfelé áramlás okozza azt, hogy a szárnyak alatt a levegő kifelé - a szárnyvégek felé - áramlik, a szárny felett az áramlás a szárny középvonala felé igyekszik. A két különböző irányú levegőréteg a kilépő mögött folyamatos örvényeket hoz létre, amely örvények közül a szárnyvégen keletkező a legerősebb.

Az indukált ellenállás az eddig megismert ellenállások (súrlódási, alaki, indukált) közül a legnagyobb. Az indukált ellenállás a fesztáv növelésével jelentősen csökkenthető.

A fesztáv növelésének határait később még vizsgáljuk.

Az oldalviszony

A szárny karcsúságát az “oldalviszony” fogalmával fejezzük ki. Például az 1:10 - es oldalviszony azt jelenti hogy a szárny “hossza” - (fesztávolsága) - tízszerese a szárnymélységnek (a szárnyszelvény hosszának.)

Ez téglalap alakú szárny esetén kifogástalan, de eltérő alaprajzú szárnyaknál már nem használható.

Ha az oldalviszonyt tört alakban fejezzük ki, akkor

Ha a téglalap szárny szélességét “a”-val, a fesztávot pedig “b”-vel jelöljük, az oldalviszony , a tört értéke nem változik ha a számlálót és a nevezőt ugyanazzal a számmal megszorozzuk. Ez a szorzó legyen most “b”, tehát a szorzás után: Ebben az alakban a tört számlálója - az “a.b” szorzat a téglalap alakú szárny felületét jelenti, a szorzat pedig a fesztávolság négyzete.
A szárny felületét “A”- val jelölve az oldalviszonyt megkapjuk, ha a szárnyfelületet elosztjuk a fesztávolság négyzetével: Az oldalviszony jelölésére a l (lambda) betűt használjuk. Igy:

l

A CH 3. szám 44. oldalán látható A/2 modell fesztávolsága 2332 mm, a csillapító felülete (466 x 85 mm = 3,96 dm²), tehát a szárny felülete 30,04 dm² A számítás során mindent dm-ben számolunk:

A fesztávolság ilyen mértékű növelése csak a korszerű, nagy szilárdságú anyagok elterjedésével vált lehetővé. De bármilyen még újabb és még szilárdabb anyagokat találnak is ki, a szárnyszelvények hosszának határt szab a légerőtani hasonlóság viszonyszáma, a:

A Reynolds szám

A modellezés kezdeteinél mindenki a nagy repülőgépek kicsinyített “mását” igyekezett elkészíteni, de azok nem repültek olyan “jól” mint az eredeti, nagy méretű szerkezet. A modellezők részére csak a nagy gépek tervezése és kísérletei során kapott eredmények álltak rendelkezésre.

F. W. Schmitz német aerodinamikus 1938-40-es években végzett mérései derítették ki azt, hogy milyen összefüggés van a nagy repülőgépek és a repülőmodellek légerőtana között. A szárny körül kialakult áramlást elsősorban a leválási pont helyzete változtatja, ezt pedig a levegőmolekulák tehetetlensége és súrlódása, illetve e kettő viszonya határozza meg. Egy test mellet elhaladó levegőmolekula először gyorsul, sebessége nő, mozgási energiája nagyobb lesz. Ugyanakkor a test felületével súrlódik, ez a súrlódás fékezi, végül a levegőrészecske megáll. A megállás helye adja meg az áramlás leválásának helyét, mert az utánuk jövő levegőmolekulák is helyet akarnak “csinálni” maguknak. A levegőrészecskét a tehetetlensége tovább akarja mozgatni, a súrlódás pedig fékezi. Ez a két erő alakítja ki a test körüli áramlás képét.

Ez a meggondolás adta az ötletet Osborne Reynoldsnak (1842 - 1912) az áramlástan egyik legfontosabb szabályának megalkotásához: A geometriailag hasonló alakú testekre ható légerők arányosak, ha az áramlás képe hasonló, ha a levegőrészecskére működő tehetetlenségi és súrlódási erők hányadosa azonos.

A Reynolds szám egy bizonyos áramlásnál fellépő tehetetlenségi és súrlódási erők hányadosa.

Ennek során erőt osztunk erővel, tehát a Reynolds szám mértékegység nélküli viszony-szám.

Ezeknek az erőknek felírása egy kis levegőrészecskére, és hányadosuk kiszámítása átlagoson felüli mennyiségtani ismereteket igényel, ezért csak a közismert végeredményt kell ismerni - és felhasználni.

Ahol R = Reynolds szám
v = az áramlás sebessége m/s - ban,
t = a szárnyszelvény hossza m - ben,
n = (nű, görög betű) tartalmazza a levegő sűrűségi és súrlódási tényezőit. Ezt a légerőtanban “kinematikus nyúlóssági tényezőnek” nevezik. Ez függ a levegő állapotától: hőmérséklettől, légnyomástól. A közelítő számításoknál átlagos állandó értékkel szoktunk számolni.

A repülőmodellek esetében a Reynolds számot egy egyszerűsített képlettel is kifejezhetjük:

R = 70 x v x t

Ahol: R = Reynolds szám,
v = sebesség - m/s - ban,
T = szárnyszelvény hossza - mm (!) - ben,
70 = állandó szám (a levegő változó tulajdonságait helyettesítő állandó)

Ezek szerint az (előző részekben említett) A/2 modell Reynolds száma:

R = 70 •  4 m/s • 150 mm

R = 42.000

R = 70 • 4 m/s • 120 mm

R = 33.600

Az R szám nagyobbik szárnyszelvény-hossz esetén a nagyobb, kisebb szárnyszelvény-hossz esetén a Reynolds szám is csökken. Ezért nem lehet “akármeddig” csökkenteni a szárnyszelvények hosszát. Jelenlegi ismereteink szerint a ma használatos fesztávolságok (és szárnyszelvények) esetén közel vagyunk az elméletileg lehetséges határhoz.

Néhány Reynolds - szám a természetből:

A repülő szerkezet	Szárnymélység mm-ben	Sebesség m/s-ban	R száma
Juharfa termése	15	1,8	1.900
Lepke	50	2	4.200
Fecske	30	7	14.700
Fecske	30	30	63.000
Sirály	140	10	89.000
Gólya	300	12	250.000

Néhány repülő “szerkezet”:

Vitorlázó repülőgép	900	16	1.000.000
Motoros sportrepülőgép	1.300	55	5.000.000
Utasszállító repülőgép	5.000	92	32.000.200
Hangsebességű vadászgép	3.000	330	70.000.000

A kritikus Reynolds szám

Ezek alapján érthető hogy egy vitorlázó repülőgép ( R = 1.000.000) kicsinyítve, ugyanazzal a szárnyszelvénnyel modellként nem repülhet.

F. W. Schmitz egyik érdekes kísérlete az volt, hogy egy kis szárnyat egyre csökkenő sebességű megfújásnál vizsgált - ezzel fokozatosan kisebb R szám mellett végezte a méréseit. Változatlan állásszög mellett végezve a kísérletet azt tapasztalta hogy egy - a vizsgált szárnyra jellemző - sebesség mellett hirtelen lecsökkent a felhajtóerő, ugyanakkor ugyanolyan hirtelen megnőtt a szárny ellenállása.

Füsttel és az áramlásba helyezett könnyű fonalakkal vizsgálva a szelvény körüli áramlást, magyarázatot is tudott adni a jelenségre. Az alacsony R számoknál a szelvények körül lamináris határréteg alakul ki. Itt aránylag a nagy felületi súrlódás miatt a határréteg gyorsan lefékeződik és az áramlás már a szelvény legvastagabb helyén elválik a felülettől. Az áramvonalak nem követik a szelvény alakját, e miatt csökken a felhajtóerő, a leválási pont után kialakuló vastag örvénytér pedig az ellenállást növeli meg jelentősen.

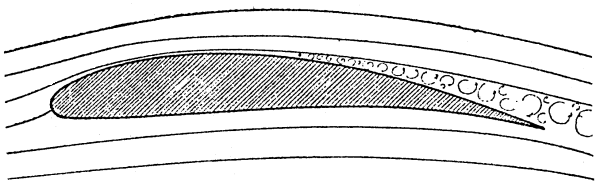
Nagyobb R számoknál - ami azt jelenti hogy a levegőrészecskéknek nagyobb a tehetetlenségi erő és súrlódási erő hányadosa - a súrlódás befolyása csökken és az áramvonalak jobban megközelítik a testet - illetve hosszabb darabon, tovább a szárnyszelvény közelében maradnak.

Így a szelvényhez jobban simuló áramvonalak nagyobb felhajtó erőt és kisebb ellenállást biztosítanak. Itt a leválás lényegesen hátrább következik be, a szelvény tulajdonságai kedvezőbbek.

Schmitz mérései szerint - az akkori modelleknél használt - 12% vastag szelvényeknél az áramlás-leválás 60 -70.000 R számnál következett be, egy másik, abnormálisan vastag szárnyszelvénynél ugyanez kb. 100.000 R számnál alakult ki.

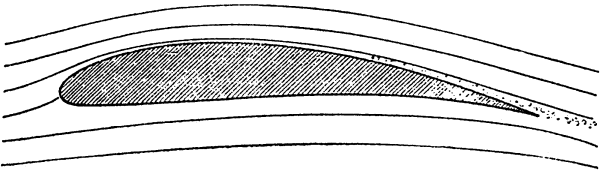
Ezekből azt a következtetést vonta le hogy minden szárnyszelvénynek van egy jellemző R száma, amelynél nagyobb R számmal szépen és jól repül, de ugyanez a szárny az adott szelvényre jellemző R szám alatt nagyon gyenge eredményeket ér el.

Ezt a - szárnyszelvényre jellemző - R számot Schmitz

kritikus Reynolds számnak (R_k)

nevezte el. Mérései szerint a várható repülési sebesség és a modell tervezett méretei alapján olyan szelvényt kell választani, amelynek kritikus R száma alacsonyabb, mint a repülés közben fellépő R szám.

Kísérletei során 3% vastagságú szelvényeket is vizsgált, és ezeknél a kritikus R számot 20 - 50.000 közöttinek mérte.

Ismét a füsttel végzett határréteg-vizsgálat derítette ki ennek okát. Ezeknél a torlópont valamivel a szelvény orrpontja alatt alakul ki. A levegőnek ezért élesen meg kell kerülnie a szelvény orrát.Az éles belépőél esetén szükséges erős irányváltozást a levegő nem képes követni és már a szelvény orrpontjánál kissé leválik. A leválás következtében erős kis él-örvény keletkezik, amely a határréteget megzavarja, kezdettől fogva turbulenssé teszi. A turbulens határréteg pedig - mivel a külső rétegek részecskéi a belsőkbe is átvándorolnak, és ott sorozatos ütközésekkel sebességüket átadják - egészen jól képes követni a szelvény alakját, a szelvény mögött csak egészen csekély örvénylés alakul ki.

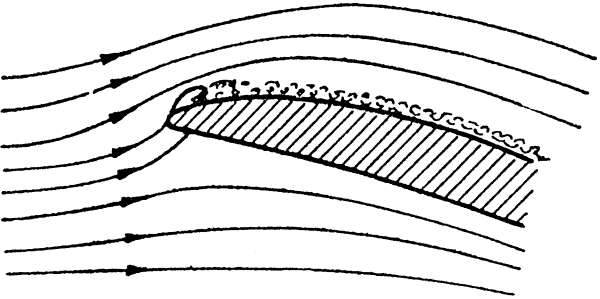
Bár a turbulens határréteg nagyobb súrlódási ellenállást jelent, ezt az ellenállás-növekedést többszörösen visszanyerjük azáltal hogy az áramlás leválása jóval később következik be és a szelvény felett nem alakul ki a nagy ellenállást jelentő örvénylő tér.

A természetben előforduló repülés adatai közül feltűnhet hogy a modelleknél előforduló Reynolds számokkal a madarak repülése során találkozhatunk. A kutatók feltételezték hogy a közismerten jól repülő madarak Reynolds számuk szerint a legjobb szárnyszelvényekkel rendelkeznek, célszerűnek látszott a modellekhez is a madarakéhoz hasonló szárnyszelvényeket használni.

A madarak és a modellek áramlástani hasonlóságára már Schmitz is felhívta a figyelmet. A modellekhez megfelelő szelvényeket a kísérletekkel foglalkozó intézeteknél alig lehetett találni, kézenfekvő volt a következő feladat: kifejezetten modellek részére kellett szárnyszelvényeket tervezni.

Ezt a feladatot - egymásról nem tudva egy időben - 1943-ban - oldotta meg a dán Sigurd Isacson és Benedek György. Mindketten repülőmodellek részére szerkesztettek szelvény-rendszert különböző vastagságokkal és íveltségekkel. A dán szelvények S.I. jelűek, a magyar szelvények B jelzésűek a tervezők nevének kezdőbetűiről.
A szelvények számjelzései is hasonlóak, csak az alkalmazott számok rendszere más. Mindkét tervező számjelzéseiben szerepelnek a szelvények főbb adatainak %-os értékei.

A kritikus Reynolds szám alatt az ellenállás hirtelen nő, a felhajtóerő hirtelen csökken, a kritikus R. szám felett kicsi az ellenállás, nagy a felhajtóerő.

A CH 3. szám 24. oldalán már megismerkedtünk egy diagrammal, amely a felhajtóerő-tényezőt és az ellenállás-tényezőt ábrázolta együtt - az állásszög függvényében.

Ha a koordináta rendszerben az ellenállást az egyik, a felhajtóerőt a másik tengelyen ábrázoljuk, e kettő közötti összefüggést szemléltető görbe a Lilienthal - féle

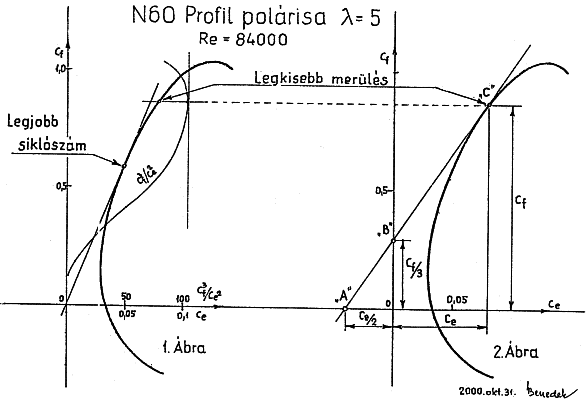
Poláris diagram

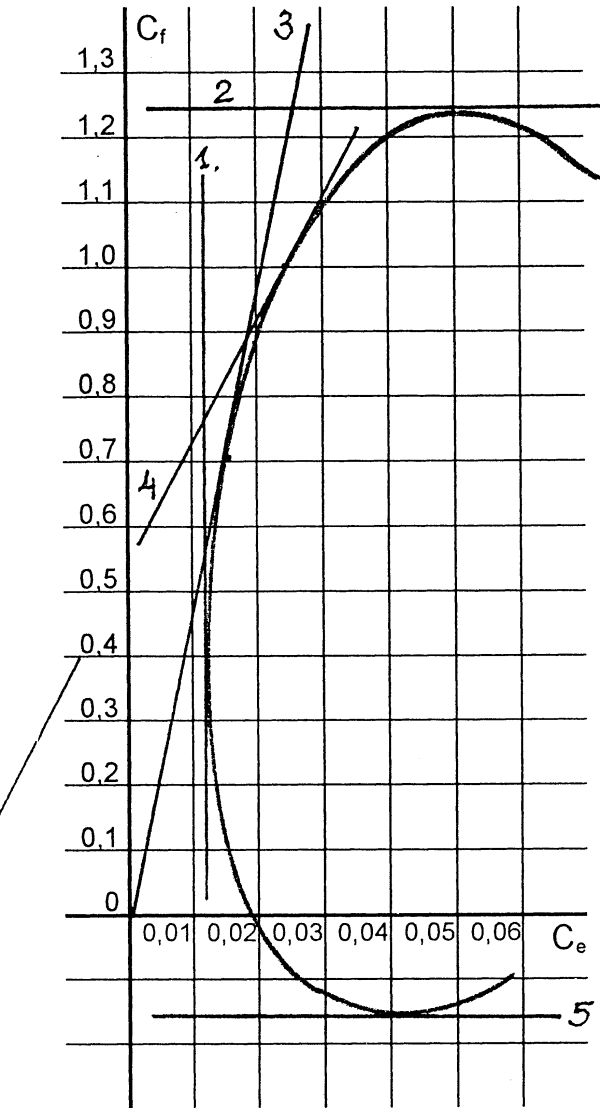
Az ellenállás - a felhajtóerőhöz képest - csekély, ezért - hogy szemléletesebb görbét kapjunk, az ellenállás léptékét - ezen az ábrán - tízszer nagyobbra vettük a felhajtóerőjénél. A görbe nevezetes pontjairól több fontos érték olvasható le.

1. A görbéhez húzott függőleges érintő adja a legkisebb ellenállást.

2. A görbe felső - vízszintes - érintője a legnagyobb felhajtóerő helye.

3. A legjobb siklószám értékét a kezdőpontból a görbéhez húzott érintő jelöli ki.

4. A legjobb siklószám helyéhez tartozó C_f felhajtóerő-tényező harmad részét megjelöljük az Y tengelyen. Ebből a pontból húzott érintő jelöli ki a legkisebb merülősebesség értékét.

5. A görbe alsó - vízszintes - érintője a hátonrepülés helye.

A kísérleti intézetek a szárnyszelvények adatait mindig végtelen oldalviszonyra (l =) adják meg. A gyakorlatban épített modellek oldalviszonya mindig véges. Ha a görbét véges oldalviszonyra számítjuk át, a görbe jobbra tolódik el. Az eltolódás mértéke az oldalviszonytól függ és az indukált ellenállás mértékével tolódik jobbra.

A szelvényekről készített poláris diagramokat általában különböző Reynolds számokra adják meg. Az így készült mérések eredményeit könnyebben tudjuk a gyakorlatban felhasználni.

A mellékelt - ma már nem korszerű de pontosan megmért - N 60 szelvény görbéjén lehet jól látni a gyakorlati felhasználás szempontjából a nevezetes pontokat.

R = 84 000  l = 5

A legkisebb merülési pont a KLEMPERER - féle módszerrel - közelítőleg - grafikusan is megállapítható. A polárgörbéhez olyan érintőt kell húzni, amely a függőleges tengelyt a keresett pont C_f értékének 1/3-nál metszi, a vízszintes tengelyt pedig a C_e érték felénél. A keresett pontot “C” betű, a tengelyek metszéspontjait az “A” és a “B” jelzi. Ez az eljárás geometriailag elég határozatlan, mert különféle érintőkkel történő próbálkozásnál valamennyi pont koordinátái egy időben változnak.

Megoldás úgy érhető el, hogy a polárgörbéhez addig húzunk érintőket, amíg a jelzett 3 pont koordinátái az előzőkben részletezett feltételeknek megfelelnek.

A modell siklása

A siklószög (j )

A repülőmodellek legfontosabb repülési formája a siklás. Bármilyen szabadon repülő modellről is legyen szó, repülési idejének legnagyobb részét a sikló repülés teszi ki.

Siklásnál a modell egyenletes sebességgel kicsi szögben merül, közeledik a földhöz. Elméletileg egyenes vonalú, egyenletes mozgást végez. A gépre ható erők egymással éppen egyensúlyban vannak. Siklás közben csak három erő hat a modellre:

1. A súlyerő, (G)

2. A felhajtóerő, (F)

3. Az ellenállás. (E)

Az ábra erősen túlozva mutatja a siklást, azért hogy az egyes szögek jobban ábrázolhatók legyenek. A valóságban a jó modell siklószöge ennél sokkal kisebb.

Az erők egyensúlya azt jelenti hogy a három erőt irány és nagyság szerint összeadva eredményül nullát kell kapnunk.

A modell annál jobb, minél kisebb szög alatt tud siklani.

Azt a szöget, amellyel a modell a földet megközelíti, siklószögnek nevezzük és “j ”- vel jelöljük.

Ha a modell sebességének vízszintes összetevőjét “v” - vel, a függőleges összetevőjét “w” - vel jelöljük, e két erő hányadosa a siklószög tangensét adja.

Ha ugyanezt az ellenállást (E) összetevőivel írjuk fel,

ahol E = a repülő szerkezet összes ellenállása
q = (vagy F_torló) - a torlónyomás (N/m² - ben)
A = a homlokfelület (a test áramlási irányra merőleges felülete) - m² - ben
C_e = az ellenállás - tényező

A felhajtóerőt is írjuk fel kiszámításának módja szerint:

ahol: F = az összes felhajtóerő
q = (vagy F_torló) - a torlónyomás - N/m² - ben
A = a homlokfelület (a test áramlási irányra merőleges felülete) - m² - ben
C_f = a felhajtóerő - tényező

A képletbe a fenti összefüggéseket felírva:

ha q.A - val egyszerűsítjük, marad:

tehát a modell siklószögét az összes ellenállás és az összes felhajtóerő hányadosának tangense adja (ami azonos a függőleges sebesség és a vízszintes sebesség hányadosával.) Képlet-szerűen felírva:

A siklószög - a j - a gyakorlatban nagyon kicsi szög.

Példa:

A modell 50 m magasságból 180”- et siklik, akkor 1 másodperc alatt

a magasságvesztése. Vízszintes sebessége (az előző esetekben vett példákkal egyezően) 4 m/s. akkor az 1” alatt megtett út = 4 m, a magasságvesztés 0,277 m, a siklószög ebből:

Ez az érték, mint szög, nem mérhető.

Az, hogy a modell 3 fokos vagy 4 fokos szög alatt siklik, ez nem sokat jelent számunkra. Sokkal könnyebben lemérhető érték

A siklószám

amely azt adja meg, hogy a modell 1 méter magasságból milyen messze képes elsiklani.

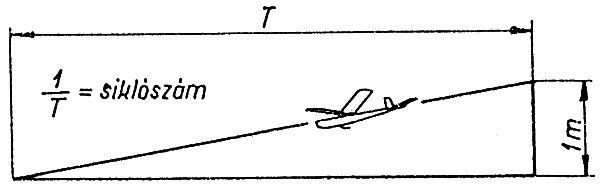
A siklószám a siklószög tangense olyan tört alakban, amelyiknek a számlálója 1. (A siklószög -j - az ábrán mindkét bevonalazott háromszögben megtalálható - mert ezek merőleges szárú háromszögek.)

Az előző példában említett modell siklószáma ha:

0,2777 m magasról 4 m távolságra siklik, akkor

1,0 m magasról távolságra jut el, tehát a “siklószáma: 14,4”

A siklószám a modell légerőtani “hatásfoka”, ami megadja a káros légellenállás és a hasznos felhajtóerő viszonyát. Példánk esetén a 14,4 - es siklószám azt jelenti hogy a modellen keletkező felhajtóerő 14,4 - szerese az ellenállásának.

A gyakorlatban időtartam repülési feladatok alapján értékelik a versenyeket, tehát nem a minél messzebbre siklás a követelmény hanem a lehető leghosszabb időtartamú repülés. Az a modell marad tovább a levegőben, amelyik a legkevésbé merül, vagyis a legkisebb az időegységre (s) jutó merülése.

A sebesség függőleges összetevője a merülősebesség. Ez a vízszintes sebesség és a siklószám ismeretében számítható ki.

<< előző rész  |  következő rész >>