4.1 Modify Algorithms 4.1, 4.2, and 4.3 so that they work for any number of processes, not just the powers of 2.
4.2 Section 4.1 presents the recursive doubling algorithm for one-to-all broadcast, for all three networks (ring, mesh, hypercube). Note that in the hypercube algorithm of Figure 4.6, a message is sent along the highest dimension first, and then sent to lower dimensions (in Algorithm 4.1, line 4, i goes down from d - 1 to 0). The same algorithm can be used for mesh and ring and ensures that messages sent in different time steps do not interfere with each other.
Let's now change the algorithm so that the message is sent along the lowest dimension first (i.e., in Algorithm 3.1, line 4, i goes up from 0 to d - 1). So in the first time step, processor 0 will communicate with processor 1; in the second time step, processors 0 and 1 will communicate with 2 and 3, respectively; and so on.
What is the run time of this revised algorithm on hypercube?
What is the run time of this revised algorithm on ring?
For these derivations, if k messages have to traverse the same link at the same time, then assume that the effective per-word-transfer time for these messages is ktw.
4.3 On a ring, all-to-all broadcast can be implemented in two different ways: (a) the standard ring algorithm as shown in Figure 4.9 and (b) the hypercube algorithm as shown in Figure 4.11.
What is the run time for case (a)?
What is the run time for case (b)?
If k messages have to traverse the same link at the same time, then assume that the effective per-word-transfer time for these messages is ktw. Also assume that ts = 100 x tw.
Which of the two methods, (a) or (b), above is better if the message size m is very large?
Which method is better if m is very small (may be one word)?
4.4 Write a procedure along the lines of Algorithm 4.6 for performing all-to-all reduction on a mesh.
4.5 (All-to-all broadcast on a tree) Given a balanced binary tree as shown in Figure 4.7, describe a procedure to perform all-to-all broadcast that takes time (ts + twmp/2) log p for m-word messages on p nodes. Assume that only the leaves of the tree contain nodes, and that an exchange of two m-word messages between any two nodes connected by bidirectional channels takes time ts + twmk if the communication channel (or a part of it) is shared by k simultaneous messages.
4.6 Consider the all-reduce operation in which each processor starts with an array of m words, and needs to get the global sum of the respective words in the array at each processor. This operation can be implemented on a ring using one of the following three alternatives:
All-to-all broadcast of all the arrays followed by a local computation of the sum of the respective elements of the array.
Single node accumulation of the elements of the array, followed by a one-to-all broadcast of the result array.
An algorithm that uses the pattern of the all-to-all broadcast, but simply adds numbers rather than concatenating messages.
For each of the above cases, compute the run time in terms of m, ts, and tw.
Assume that ts = 100, tw = 1, and m is very large. Which of the three alternatives (among (i), (ii) or (iii)) is better?
Assume that ts = 100, tw = 1, and m is very small (say 1). Which of the three alternatives (among (i), (ii) or (iii)) is better?
4.7 (One-to-all personalized communication on a linear array and a mesh) Give the procedures and their communication times for one-to-all personalized communication of m-word messages on p nodes for the linear array and the mesh architectures.
Hint: For the mesh, the algorithm proceeds in two phases as usual and starts with the source distributing pieces of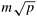 
words among the 
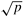nodes in its row such that each of these nodes receives the data meant for all the 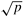nodes in its column.
4.8 (All-to-all reduction) The dual of all-to-all broadcast is all-to-all reduction, in which each node is the destination of an all-to-one reduction. For example, consider the scenario where p nodes have a vector of p elements each, and the i th node (for all i such that 0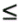 
i < p) gets the sum of the i th elements of all the vectors. Describe an algorithm to perform all-to-all reduction on a hypercube with addition as the associative operator. If each message contains m words and tadd is the time to perform one addition, how much time does your algorithm take (in terms of m, p, tadd, ts and tw)?
Hint: In all-to-all broadcast, each node starts with a single message and collects p such messages by the end of the operation. In all-to-all reduction, each node starts with p distinct messages (one meant for each node) but ends up with a single message.
4.9 Parts (c), (e), and (f) of Figure 4.21 show that for any node in a three-dimensional hypercube, there are exactly three nodes whose shortest distance from the node is two links. Derive an exact expression for the number of nodes (in terms of p and l) whose shortest distance from any given node in a p-node hypercube is l.
4.10 Give a hypercube algorithm to compute prefix sums of n numbers if p is the number of nodes and n/p is an integer greater than 1. Assuming that it takes time tadd to add two numbers and time ts to send a message of unit length between two directly-connected nodes, give an exact expression for the total time taken by the algorithm.
4.11 Show that if the message startup time ts is zero, then the expression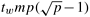 
for the time taken by all-to-all personalized communication on a 
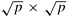mesh is optimal within a small ( 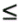4) constant factor.
4.12 Modify the linear array and the mesh algorithms in Sections 4.1-4.5 to work without the end-to-end wraparound connections. Compare the new communication times with those of the unmodified procedures. What is the maximum factor by which the time for any of the operations increases on either the linear array or the mesh?
4.13 (3-D mesh) Give optimal (within a small constant) algorithms for one-to-all and all-to-all broadcasts and personalized communications on a p1/3 x p1/3 x p1/3 three-dimensional mesh of p nodes with store-and-forward routing. Derive expressions for the total communication times of these procedures.
4.14 Assume that the cost of building a parallel computer with p nodes is proportional to the total number of communication links within it. Let the cost effectiveness of an architecture be inversely proportional to the product of the cost of a p-node ensemble of this architecture and the communication time of a certain operation on it. Assuming ts to be zero, which architecture is more cost effective for each of the operations discussed in this chapter - a standard 3-D mesh or a sparse 3-D mesh?
4.15 Repeat Problem 4.14 when ts is a nonzero constant but tw = 0. Under this model of communication, the message transfer time between two directly-connected nodes is fixed, regardless of the size of the message. Also, if two packets are combined and transmitted as one message, the communication latency is still ts.
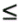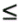4.16 (k-to-all broadcast) Let k-to-all broadcast be an operation in which k nodes simultaneously perform a one-to-all broadcast of m-word messages. Give an algorithm for this operation that has a total communication time of ts log p + twm(k log(p/k) + k - 1) on a p-node hypercube. Assume that the m-word messages cannot be split, k is a power of 2, and 1 k p.
4.17 Give a detailed description of an algorithm for performing all-to-one reduction in time 2(ts log p + twm(p - 1)/ p) on a p-node hypercube by splitting the original messages of size m into p nearly equal parts of size m/p each.
4.18 If messages can be split and their parts can be routed independently, then derive an algorithm for k-to-all broadcast such that its communication time is less than that of the algorithm in Problem 4.16 for a p-node hypercube.
4.19 Show that, if m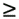 
p, then all-to-one reduction with message size m can be performed on a p-node hypercube spending time 2(ts log p + twm) in communication.
Hint: Express all-to-one reduction as a combination of all-to-all reduction and gather.
4.20 (k-to-all personalized communication) In k-to-all personalized communication, k nodes simultaneously perform a one-to-all personalized communication (1 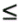k 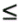p) in a p-node ensemble with individual packets of size m. Show that, if k is a power of 2, then this operation can be performed on a hypercube in time ts (log( p/k) + k - 1) + twm(p - 1).
4.21 Assuming that it takes time tr to perform a read and a write operation on a single word of data in a node's local memory, show that all-to-all personalized communication on a p-node mesh (Section 4.5.2) spends a total of time trmp in internal data movement on the nodes, where m is the size of an individual message.
Hint: The internal data movement is equivalent to transposing a 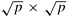array of messages of size m.
4.22 Show that in a p-node hypercube, all the p data paths in a circular q-shift are congestion-free if E-cube routing (Section 4.5) is used.
Hint: (1) If q > p/2, then a q-shift is isomorphic to a (p - q)-shift on a p-node hypercube. (2) Prove by induction on hypercube dimension. If all paths are congestion-free for a q-shift (1 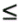q < p) on a p-node hypercube, then all these paths are congestion-free on a 2 p-node hypercube also.
4.23 Show that the length of the longest path of any message in a circular q-shift on a p-node hypercube is log p - g(q), where g(q) is the highest integer j such that q is divisible by 2j.
Hint: (1) If q = p/2, then g(q) = log p - 1 on a p-node hypercube. (2) Prove by induction on hypercube dimension. For a given q, g(q) increases by one each time the number of nodes is doubled.
4.24 Derive an expression for the parallel run time of the hypercube algorithms for one-to-all broadcast, all-to-all broadcast, one-to-all personalized communication, and all-to-all personalized communication adapted unaltered for a mesh with identical communication links (same channel width and channel rate). Compare the performance of these adaptations with that of the best mesh algorithms.
4.25 As discussed in Section 2.4.4, two common measures of the cost of a network are (1) the total number of wires in a parallel computer (which is a product of number of communication links and channel width); and (2) the bisection bandwidth. Consider a hypercube in which the channel width of each link is one, that is tw = 1. The channel width of a mesh-connected computer with equal number of nodes and identical cost is higher, and is determined by the cost metric used. Let s and s' represent the factors by which the channel width of the mesh is increased in accordance with the two cost metrics. Derive the values of s and s'. Using these, derive the communication time of the following operations on a mesh:
One-to-all broadcast
All-to-all broadcast
One-to-all personalized communication
All-to-all personalized communication
Compare these times with the time taken by the same operations on a hypercube with equal cost.
