4.1. Szabályos testek száma
 |  |  |
 | 5 szabályos test létezik. |  |
Tétel: Öt szabályos test létezik.
Bizonyítás:
Tekintsünk egy tetszőleges konvex poliédert, ésvezessük be a következő jelöléseket!
Lapok száma: l.
Csúcsok száma: c.
Élek száma: e.
Egy lapon lévő élek száma: n.
Egy csúcsba futó élek száma: m.
Ekkor igazak az alábbi összefüggések (egyszerűkombinatorikai gondolatmenet miatt):
Figyelembe véve azt, hogy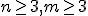 
, a következő öt lehetőséget kapjuk:
|
| n | m | e | l | c | Test |
| 1. | 3 | 3 | 6 | 4 | 4 | Tetraéder |
| 2. | 3 | 4 | 12 | 8 | 6 | Oktaéder |
| 3. | 3 | 5 | 30 | 20 | 12 | Ikozaéder |
| 4. | 4 | 3 | 12 | 6 | 8 | Hexaéder |
| 5. | 5 | 3 | 30 | 12 | 20 | Dodekaéder |
Felhasználtuk, hogy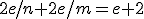 
összefüggés adódik azEuler-tételből, így 
.)
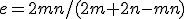Még végig kell gondolnunk, hogy ilyen paraméterűpoliéderek tényleg vannak, származtathatók.
A hexaéder e már jól ismert kocka. Belőleszármaztatható a tetraéder, az oktaéder. Az oktaéderből ikozaéder, abból pediga dodekaéder.