6.1 Describe a message-transfer protocol for buffered sends and receives in which the buffering is performed only by the sending process. What kind of additional hardware support is needed to make these types of protocols practical?
6.2 One of the advantages of non-blocking communication operations is that they allow the transmission of the data to be done concurrently with computations. Discuss the type of restructuring that needs to be performed on a program to allow for the maximal overlap of computation with communication. Is the sending process in a better position to benefit from this overlap than the receiving process?
6.3 As discussed in Section 6.3.4 the MPI standard allows for two different implementations of the MPI_Send operation - one using buffered-sends and the other using blocked-sends. Discuss some of the potential reasons why MPI allows these two different implementations. In particular, consider the cases of different message-sizes and/or different architectural characteristics.
6.4 Consider the various mappings of 16 processors on a 4 x 4 two-dimensional grid shown in Figure 6.5. Show how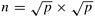 
processors will be mapped using each one of these four schemes.
6.5 Consider Cannon's matrix-matrix multiplication algorithm. Our discussion of Cannon's algorithm has been limited to cases in which A and B are square matrices, mapped onto a square grid of processes. However, Cannon's algorithm can be extended for cases in which A, B, and the process grid are not square. In particular, let matrix A be of size n x k and matrix B be of size k x m. The matrix C obtained by multiplying A and B is of size n x m. Also, let q x r be the number of processes in the grid arranged in q rows and r columns. Develop an MPI program for multiplying two such matrices on a q x r process grid using Cannon's algorithm.
6.6 Show how the row-wise matrix-vector multiplication program (Program 6.4) needs to be changed so that it will work correctly in cases in which the dimension of the matrix does not have to be a multiple of the number of processes.
6.7 Consider the column-wise implementation of matrix-vector product (Program 6.5). An alternate implementation will be to use MPI_Allreduce to perform the required reduction operation and then have each process copy the locally stored elements of vector x from the vector fx. What will be the cost of this implementation? Another implementation can be to perform p single-node reduction operations using a different process as the root. What will be the cost of this implementation?
6.8 Consider Dijkstra's single-source shortest-path algorithm described in Section 6.6.9. Describe why a column-wise distribution is preferable to a row-wise distribution of the weighted adjacency matrix.
6.9 Show how the two-dimensional matrix-vector multiplication program (Program 6.8) needs to be changed so that it will work correctly for a matrix of size n x m on a q x r process grid.
