Rekurzív
szabályokat a sorozatoknál általánosabb függvényekre is
meg lehet adni, de ilyen szabályokkal az iskolában nem foglalkozunk.
Amikor adva vannak egy függvény bizonyos helyeken vett értékei
vagyis bemenő és a nekik megfelelő kijövő adatok, akkor
a függvény szabályán olyan utasítást értünk, amelyet követve
mindegyik bemenő adattól éppen a neki megfelelő kijövő adatig
jutunk el. Ilyen utasítást adnak meg a sorozatok n n -edik
tagjára kapott képletek. Ilyent adnak meg a fejezet második
ábráján látható nyilak is.
Ahogy a véges
sorozatokat nemcsak egyféle szabály szerint lehet végtelen
sorozatokká kiterjeszteni, úgy a függvényekhez sem csak
egyféle szabályt találhatunk, amely mindegyik bemenő adattól
éppen a neki megfelelő kijövő adathoz vezet. Erre az általános
esetre is érvényes tehát az a megjegyzés, hogy a szabály
helyett mindig egy szabályt keresünk a sok közül, vagy nem
is egyet, hanem lehetőleg többet, ha már egyszer úgyis tudjuk,
hogy több van.
Ha a függvény
bemenő és kijövő adata is egyetlen szám (például: Be 3,
Ki 5), akkor a gyerekek is könnyen találnak sok olyan szabályt,
amely ezt a hozzárendelést létesíti. Példaképpen megadunk
itt néhányat:
x 3 y 5 y=x+2 y=8 x y=x24 y=(15/x) y=2x1 y=112x y=2x2 13
y=(20/x+1) y=3x4 y=14 3x y=2x3
x 3 y 5 y = x + 2 y = 8 - x y = x 2 4 y = 15 x y = 2 x 1
y = 11 2 x y = 2 x 2 13 y = 20 x + 1 y = 3 x 4 y = 14 3
x y = 2 x 3
Ha nemcsak egész
számokra gondolunk, hanem bármilyen pozitív vagy negatív
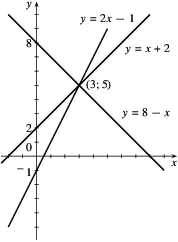
számokra, akkor ezek egy-egy vonal egyenletei. (Néhányat
közülük a következő ábrán láthatunk.) Az utolsó két oszlopban
levők görbe vonalak egyenletei. Néhány pontjuk ábrázolásával
a tanulók megsejthetik, hogy melyik esetben vannak a pontok
egy egyenesen, melyik esetben nem. Semmit sem kell tudniuk
az exponenciális függvényről, elég ismerniük a hatványjelölés
értelmét ahhoz, hogy három helyen ábrázolva a 2 x 2 x kifejezés
által felvett értékeket, észrevegyék, hogy ezek nincsenek
egy egyenesen. Meglepő módon az egyszerűbbnek tűnő eset
okoz több gondot: azt, hogy az első két oszlopban levő és
más hasonló típusú egyenletek grafikonja egyenes, megsejteni
könnyű, de belátni sokkal nehezebb, mint a többiről azt,
hogy nem egyenes a grafikonjuk. Harmadikként még megkülönböztethetjük
azokat az egyváltozós szám szám függvényeket, amelyeknek
a grafikonja nem egyetlen egyenes ugyan, de csak egyenes
vonalakból félegyenesekből, szakaszokból áll. Ilyen például
az abszolútérték függvény. Ezeket szakaszonként lineáris
függvényeknek nevezzük.
 |
|
A rövidség kedvéért
beszéltünk itt egyenletekről és mindegyiknek a grafikonjáról.
Ha pontosabbak akarunk lenni, akkor azoknak a függvényeknek
a grafikonjáról kell beszélnünk, amelyeket ezek a kétismeretlenes
egyenletek megadnak, olyan értelemben, hogy x x meghatározott
értékeihez y y -nak egy-egy értékét rendelik. (Maguk a jobb
oldalon álló csak az x x ismeretlent tartalmazó kifejezések
is megadják ezt a hozzárendelést, tekintve, hogy a bal oldalon
egyedül áll az y y .) Másképpen azt mondhatjuk, hogy ezeknek
a kétismeretlenes egyenleteknek a megoldásai más szóval:
gyökei számpárok, és a grafikonok azokból a pontokból állnak,
amelyeknek a koordinátái ezek a számpárok, vagyis a grafikonok
ezeknek a kétismeretlenes egyenleteknek a gyökeit ábrázolják.