11. A matematika

Oktatási segédanyagok

• Matematika 9. – Út a tudáshoz (MX-226) (Pdf 35 MB)
• Matematika 10. – Út a tudáshoz (MX-265) (Pdf 20 MB)
• Matematika 11. – középszint – Út a tudáshoz (MX-267) (Pdf 38 MB)
• Matematika 12. – középszint – Út a tudáshoz (MX-269) (Pdf 18 MB)
• Matematika 11-12. – emelt szint – Út a tudáshoz (MX-350) (Pdf 32 MB)

• Czapáry Endre - Korom Pál: Matematika gyakorló feladatlapok 9. (Pdf 3 MB)
• Czapáry Endre - Korom Pál: Matematika gyakorló feladatlapok 10. (Pdf 6 MB)
• Korom Pál: Matematika gyakorló feladatlapok 11. (Pdf 5 MB)
• Korom Pál: Matematika gyakorló feladatlapok 12. (Pdf 3 MB)

• Érthető matematika 9. megoldások (Pdf 3 MB)
• Érthető matematika 10. megoldások (Pdf 3 MB)
• Heuréka 9. megoldások (Pdf)
• Heuréka 10. megoldások (Pdf 3 MB)
• Heuréka 11. megoldások (Pdf)

• Érettségi feladatsorok és új minta feladatsorok megoldásokkal
• Középszintű tematikus feladatsorok, 2003 - 2017. október (Pdf 22 MB)

• Nemzeti Köznevelési Portál
• Mateking.hu Ideiglenesen ingyenes! Ne regisztráljatok, csak használjátok! Érettségi felkészítő is!
• Sulinet Tudásbázis

A tanórák anyagai

A tananyaggal kapcsolatos kérdéseket, ill. a feladatok megoldását, az esetleges beadandó anyagokat a fenti e-mail címre küldjétek! A honlapon szereplő "táblaképek" tartalmát mindig írjátok be a füzetbe! A házi feladatok megoldását a megadott időre, kézírással, a füzetből lefényképezve kérem!

• 2020.03.16. 73. óra

  Két egyenes metszéspontjának meghatározása, a háromszög nevezetes pontjai

  
  
  
• 2020.03.18. 74. óra

  Az egyenes egyenlete, egyenesek metszéspontja, gyakorlás

  Az Oktatási segédanyagok között a Nemzeti Köznevelési Portál most megújított oldalán megtaláljátok az OFI Matematika tankönyvek új interaktív okostankönyv változatait. A 11. osztályos Matematika tankönyvben a 78. fejezettől foglalkozik az egyenes egyenletével. Ha nem találnátok meg, itt egy közvetlen link: Az egyenes egyenlete. Önállóan dolgozzátok fel a tananyagot, végezzétek el az összes interaktív feladatot, a házi feladatokat pedig a füzetetekben oldjátok meg, és lefényképezve küldjétek el csütörtökig a fenti címre.
  
  Segítség: a 3. házi feladatban írjátok fel mindhárom felezőmerőleges egyenletét, majd nézzétek meg, azonos-e valamelyik (esetleg átalakítás után, pl. beszorzás, leosztás, átrendezés) a megadott egyenlettel.
  
  Újdonság!
  Nézzétek meg és dolgozzátok fel a most ingyenessé tett Mateking.hu honlap Az egyenes egyenlete, egyenesek metszéspontja című fejezetét!
  Különösen ajánlom a hiányzóknak vagy akik nem értették meg eléggé órán a tananyagot. Egy tanár mindent elmagyaráz lépésről lépésre dinamikus ábrák segítségével. Saját ütemben a lap szélén levő nyilakra kattintva lehet előre- vagy visszalépni. Vagy megtekinthetitek az anyagot összefüggő videóként is. Minden benne van, amit eddig tanultunk az egyenesekről, a háromszög nevezetes pontjai is.

• 2020.03.20. 75.óra

  Pont és egyenes távolsága, Két párhuzamos egyenes távolsága

  Érthető matematika 11. tankönyv (továbbiakban Tk.) 40. fejezet, 167-168. oldal
  

  Tanulmányozzátok a két kidolgozott példát és azok alaján oldjátok meg a 168. oldal 1. és 2. feladatát. A megoldást fényképezzétek le, és a füzetképet a következő óráig küldjétek el az oldal tetején látható e-mail címemre.
  
  Figyelem!
  Úgy látom, hogy a ti tankönyvetekben egészen más feladatok vannak, mint nálam. Úgy látom, az újabb kiadásba betettek egy két oldalas olvasmányt az 55. oldalra Pénzügyi alapfogalmak (olvasmány) címmel. Emiatt utána végig 2 oldal csúszás van. Ezek szerint néhol a feladatokat is átírták.
  Idemásolom az eredeti házi feladatokat, természetesen nem kell pluszban megcsinálni holnapig.
  1. Számítsuk ki az
  a) (3,-4) pont és a 2x - y = -5 egyenes,
  b) (-2;-3) pont és az 5x + 3 y = 9 egyenes távolságát!
  2. Számítsuk ki a 12x - 5y = 1 és a 12x - 5y = -12 egyenesek távolságát!
  Segítség a 2. feladathoz: Mindkét egyenes normálvektora az n(12,-5) vektor, tehát párhuzamosak. A második egyenes az x tengelyt a T_x(-1;0) pontban metszi, elég ennek a pontnak a távolságát kiszámítani az első egyenestől. Azaz visszavezethetjük a feladatot pont és egyenes távolságának meghatározására. Ennek menete: A pontból merőlegest állítunk az egyenesre, meghatározzuk a metszéspontot, majd a P pontnak ettől való távolságát az ismert pitagoraszi távolságképlettel.
  
  Nézzétek meg a Mateking.hu honlap Pont és egyenes távolsága című fejezetét is!
  A szokásos gondolatmenet után szerepel benne egy egyszerű távolságképlet is minden magyarázat és indoklás nélkül. Nem ajánlom a használatát, mivel a sárga függvénytáblázatban nincs benne, így az érettségin is problémás lenne az alkalmazása. Különben sem támogatom a légből vett képletek használatát, módszereket, eljárásokat érdemes megtanulni.
  
  Ajánlom még az Oktatási segédanyagok közt is szereplő Sulinet Tudásbázis leckéjét, melyet közvetlenül a következő linken érhettek el: Pont és egyenes távolsága, a szögfelező nem kell.

• 2020.03.23. 76.óra
  
  
  
  
  
  
  
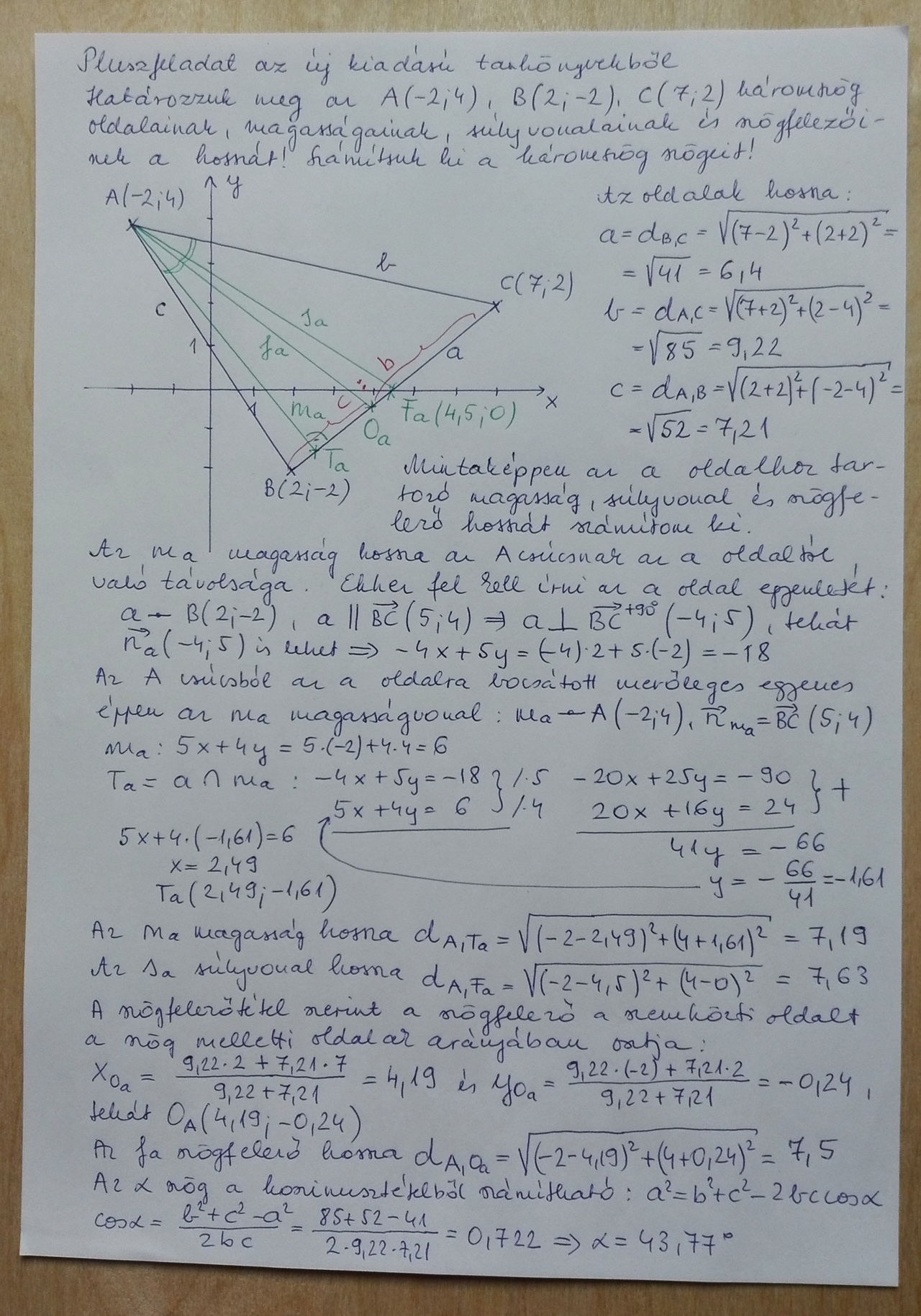
  A másik két oldalhoz tartozó magasságvonal, súlyvonal, szögfelező hosszának, a többi szög nagyságának kiszámítása, ill. a súlyvonalak és a szögfelezők egyenletének felírása szorgalmi feladatként beküldhető.
  Megjegyzés: A magasság hosszát az oldalak és a szögek ismeretében szögfüggvénnyel is ki lehet számítani, pl. sin β = m_a / c.
  

  Vegyes érettségi feladatok

  Az Oktatási segédanyagok között is szerepel a Középszintű tematikus feladatsorok, 2003 - 2017. október (Pdf 22 MB) gyűjtemény, ennek az Egyenes című fejezetét dolgozzuk fel. Ma a 133-134. oldal feladatait kell megoldanotok. Először próbáljátok mindet önállóan megoldani, de ha elakadtok, nézzétek meg a javítási útmutató megoldásait, amit dátum alapján a következő linken találtok meg: Középszintű matematika érettségi feladatsorok. A megoldásotokat a füzetetekbe írjátok be, fényképezzétek le, és a füzetképet a következő óráig küldjétek el az oldal tetején látható e-mail címemre.

• 2020.03.25. 77.óra

  Figyelem!
  Most találtam a Tankönyvkatalógusban az ingyenesen letölthető Matematika gyakorló feladatlapokat. Már most a témazáró dolgozat előtt is hasznos lehet, hiszen minden faladat viszonylag részletes megoldása megtalálható a kiadvány végén. Közvetlen link: Korom Pál: Matematika gyakorló feladatlapok 11. (Pdf 5 MB). Az aktuális témakörhöz kapcsolódó feladatok a 21-26. feladatlapokon vannak. A következő témakörtől viszont hivatalosan is használni fogjuk.

  Vegyes érettségi feladatok

  Az Oktatási segédanyagok között is szerepel a Középszintű tematikus feladatsorok, 2003 - 2017. október (Pdf 22 MB) gyűjtemény, most folytatjuk az Egyenes című fejezet feldolgozását. Ma a 135-136. oldal feladatait kell megoldanotok. Először próbáljátok mindet önállóan megoldani, de ha elakadtok, nézzétek meg a javítási útmutató megoldásait, amit dátum alapján a következő linken találtok meg: Középszintű matematika érettségi feladatsorok. A megoldásotokat a füzetetekbe írjátok be, fényképezzétek le, és a füzetképet a következő óráig küldjétek el az oldal tetején látható e-mail címemre.

• 2020.03.27. 78. óra

  Összefoglalás

  
  

  Az Oktatási segédanyagok között szerepel a Heuréka 11. megoldások (Pdf). Innen adom most a házi feladatokat: 74. oldal. 2.fejezet. 2. b feladat, 75/3/3, 77/4/2, 86/8/2/b, 86/8/3/b, 88/9/3, 89/10/2. A feladatokat a füzetetekben oldjátok meg. Ne a "gyári" megoldásokat másoljátok ki, azokat csak akkor nézzétek meg, ha elakadtok, ill. ellenőrzésre használjátok! A füzetképet a következő óráig töltsétek fel a Google Tanteremben.